Скалярные и векторные случайные величины

Случайные величины бывают скалярными и векторными. Исчерпывающей характеристикой скалярной случайной величины х является ее функция распределения вероятностей 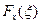, определяю­щая вероятность того, что случайная величина х примет значение, не превосходящее заданную величину , т. е.

Производная от функции распределения называется плотностью распределения или плотностью вероятности случайной величины х:

В дальнейшем для упрощения обозначений функцию распределения вероятностей обозначим через F(x), а плотность вероятности —через р(х).

Плотность р(х) скалярной случайной величины х обладает сле­дующими свойствами:

Несколько скалярных случайных величин х₁,..., х_n, рассматри­ваемых совместно, образуют векторную случайную величину х. Ее статистические свойства описываются полностью n-мерной плотно­стью вероятности р(х) =р(х₁,..., х_n).

Как и для скалярной случайной величины, плотность вероятности р(х) случайного вектора всегда неотрицательна, а соотношение (1.1) — (1.3) трансформируются в следующие:

В формуле (1.4) через обозначен n-мерный интеграл по облас­ти D в пространстве переменных х₁,..., х_n.

Зная плотность вероятности р(х) вектора х, можно определить плотности вероятности отдельных составляющих этого вектора. Пусть, например, требуется найти р(y), где , . Обозначим остальные п — R составляющих вектора х через .

Тогда

где dy = dx₁...dx_R; dz=dx_R+1...dx_n.

Плотность вероятности р(х) устанавливает вероятностную зави­симость между составляющими случайного вектора х. Эта зависи­мость может быть также охарактеризована с помощью условной плотности вероятности. Обозначим через условную плот­ность вероятности случайного вектора у размерности R при усло­вии, что случайный вектор z принял определенное значение z = Z, и через - условную плотность вероятности вектора z раз­мерности п — R при условии y=Y. Если х={у, z}, то совместная плотность р(х) связана с условными плотностями вероятности и соотношениями

где р(у) и p(z) —соответственно плотности вероятности векторов y и z.

Из формулы (1.7) с учетом (1.5) и (1.6) следуют выражения для условных плотностей вероятности

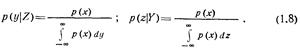
Заменяя в первом выражении в (1.8) плотность р(х) через получаем

Соотношение (1.9) называется формулой Байеса. Оно выража­ет связь между условными плотностями вероятности и . Аналогично записывается и обратная формула:

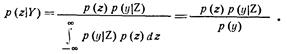
Векторные случайные величины y и z называют независимыми, если р(у, z)=p(y)p(z). Из формулы (1.7) следует, что для неза­висимых случайных векторов у и z справедливо выражение при любом y=Y и — при любом z=Z.

Если вектор х состоит из п независимых составляющих х₁,..., х_n, то плотность вероятности р(х) такого вектора равна произведению плотностей его составляющих: