Линейные и нелинейные преобразования случайных величин

При решении задач статистического анализа и оптимиза­ции управления движением летательных аппаратов часто требуется определять моменты и распределения линейных и нелинейных функ­ций случайных величин. Например, при переходе от одной системы координат к другой требуется уметь вычислить вектор математиче­ских ожиданий и корреляционную матрицу фазового вектора, опи­сывающего состояние летательного аппарата относительно новой системы координат, если статистические характеристики фазового вектора относительно исходной системы координат известны.

Вначале рассмотрим случай линейного преобразования случай­ной величины. Пусть х и у — случайные векторы, связанные между собой линейным соотношением

где х — вектор размерности п; у — вектор размерности l; А — мат­рица размерности l × п; b — неслучайный вектор размерности l.

Используя соотношение (1.11) и учитывая (1.12), находим соот­ношение между т_х и т_у:

Вычитая (1.25) из (1.24), получаем соотношение 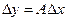между центрированными случайными величинами, из которого непосредст­венно вытекает соотношение между корреляционными матрицами К_x и К_у:

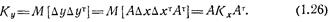
В частном случае при , т. е. когда х и у — скалярные слу­чайные величины, имеем m_y=am_x+b; D_y=a²D_x. При п=2 и l=1, т. е. если y=a₁x₁ + a₂x₂ + b, получаем m_y = a₁m₁+ a₂m₂ + b и , где K₁₁, K₁₂, K₂₂, - элементы корреляци­онной матрицы К_x-

В случае нелинейной зависимости y= f(x), где x — скаляр,

т. е. для нахождения m_y и D_y недостаточно знать т_х и D_x, а долж­на быть известна плотность вероятности р(х) аргумента х.

Пример. Рассмотрим преобразование гауссовской случайной величины х не­линейным звеном типа «реле» с уровнем насыщения А. Подставляя уравнение реле f(x)=A sign (x) и выражение для нормальной плотности вероятности (1.17)в соотношения (1.27) — (1.28) и учитывая свойства интеграла вероятно­сти (1.21), получаем

Аналитически решение задачи определения плотности вероятно­сти p(у) нелинейной функции y = f(x) от случайной величины х мо­жет быть получено лишь в том случае, когда существует взаимно однозначное соответствие между х и у, т. е. когда функция f(х) — монотонная.

Пусть f (x) монотонно возрастает. Тогда функция распределения F(y) может быть найдена с помощью соотношения

При взаимно однозначном соответствии между х и у из соотноше­ния y=f(x) можно найти обратную функцию поэтому . Дифференцирование интеграла по переменной у, входящей в верхний предел, дает

где .

При монотонном убывании f(x)

Отсюда

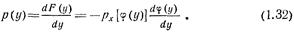
Соотношения (1.31) и (1.32) можно переписать в виде одной фор­мулы:

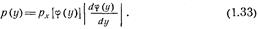
Пример. Пусть 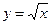, а аргумент х распределен равномерно на интервале [0, 1], т. е.

Требуется найти p(y). Поскольку в данном , то и

Отсюда

1.1.5. Характеристическая функция и семиинварианты

При решении ряда задач наряду с функцией и плотно­стью распределения вероятностей используют характеристическую функцию случайной величины. Так называют функцию , яв­ляющуюся преобразованием Фурье от плотности вероятности:

Приведем некоторые свойства характеристических функций

Если — независимые случайные величины и

Математическое ожидание и дисперсию случайной величины можно найти, используя производные от логарифма характеристи­ческой функции :

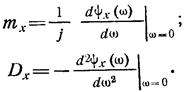
Для гауссовской случайной величины х с математическим ожи­данием т и дисперсией D

Производную R-го порядка логарифма характеристической функции в точке , умноженную на , называют семиинвариан­том R-го порядка случайной величины. Первыми двумя семиинвари­антами являются математическое ожидание и дисперсия, а семиин­вариант порядка R есть рациональная функция первых R моментов случайной величины. В частности,

где

СЛУЧАЙНЫЕ ПРОЦЕССЫ