Конкретный вид распределения случайной величины х зависит от физической природы явления. Особое место среди всевозможных распределений занимает распределение Гаусса или нормальное распределение, поскольку именно такими или близкими к нормальному являются распределения многих случайных величин, рассматриваемых при анализе движения автоматических летательных аппаратов.
Нормальная плотность вероятности р г (x) скалярной случайной величины х описывается выражением

Она полностью характеризуется двумя параметрами: тх и Dx. Пользуясь соотношениями (1.12) и (1.14), можно убедиться в том, что параметр тх нормальной плотности вероятности есть математическое ожидание, a Dx — дисперсия этой случайной величины.
В соответствии с формулой (1.2) вероятность попадания гауссовской случайной величины х в интервал 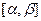 равна
равна
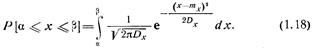
После замены переменной х на 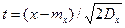 вычисление интеграла в формуле (1.18) сводится к вычислению соотношения
вычисление интеграла в формуле (1.18) сводится к вычислению соотношения
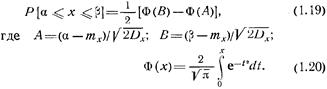
Значения функции Лапласа Ф(х), определяемой соотношением (1.20), приведены в приложении 1. При проведении расчетов на ЦВМ их можно рассчитать с помощью стандартной подпрограммы.
При преобразованиях выражений, содержащих функцию Лапласа Ф(х), можно пользоваться следующими свойствами этой функции:
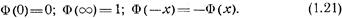
Нормальное распределение вероятностей n-мерного случайного вектора х описывается формулой
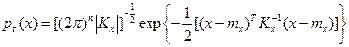
где тх — вектор математических ожиданий; Кх — корреляционная матрица; 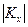 - определитель корреляционной матрицы.
- определитель корреляционной матрицы.
В евклидовом n-мерном пространстве, координатами которого являются составляющие вектора х, плотность вероятности р г (х) постоянна на концентрических гиперэллипсоидах:
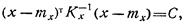
называемых гиперэллипсоидами рассеивания, где С — любое положительное число. Центром гиперэллипсоидов рассеивания является точка с координатами тх, направление главных осей совпадает с собственными векторами 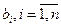 корреляционной матрицы Кх, а длина каждой из главных полуосей равна
корреляционной матрицы Кх, а длина каждой из главных полуосей равна  , где
, где 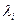 — собственное значение корреляционной матрицы Кх, соответствующее собственному вектору bi.
— собственное значение корреляционной матрицы Кх, соответствующее собственному вектору bi.
В двумерном случае нормальное распределение (1.22) принимает вид
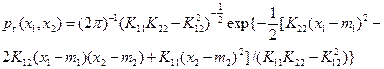 (1.23)
(1.23)
Плотность вероятности (1.23) постоянна на эллипсах, называемых эллипсами рассеивания. Угол между главной осью эллипса рассеивания и осью Ox1 определяется с помощью выражения [8]
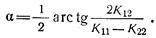
Если составляющие х1 и х2 вектора х некоррелированы, то направления главных осей эллипса рассеивания совпадают с направлениями осей системы координат Ох1х2.
На практике принято строить эллипсы рассеивания, главные полуоси которых равны 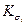 где
где 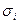 — С КО соответствующей компоненты; К — целое число.
— С КО соответствующей компоненты; К — целое число.
 2015-10-22
2015-10-22 839
839








