2015-10-22
869
Непрерывная случайная величина Х, которая может принимать как положительные, так и отрицательные значения во всем диапазоне возможных значений от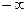 
до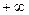 
, имеет нормальное распределение, если плотность распределения равна
f(х) =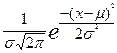 
, (2.44)
где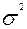 
-дисперсия случайной величины, 
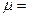М[Х] – ее математическое ожидание, е = 2,72, 
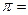3,14.
Кривая плотности распределения нормального распределения(кривая Гаусса) имеет симметричный колоколообразный вид с максимальной ординатой при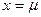 
, равной 
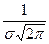. По мере удаления в обе стороны от точки 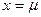плотность распределения падает и при 
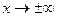кривая асимптотически приближается к оси абсцисс.
Функция нормального распределения имеет вид:
Ф(Х) =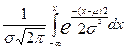 
(2.45)
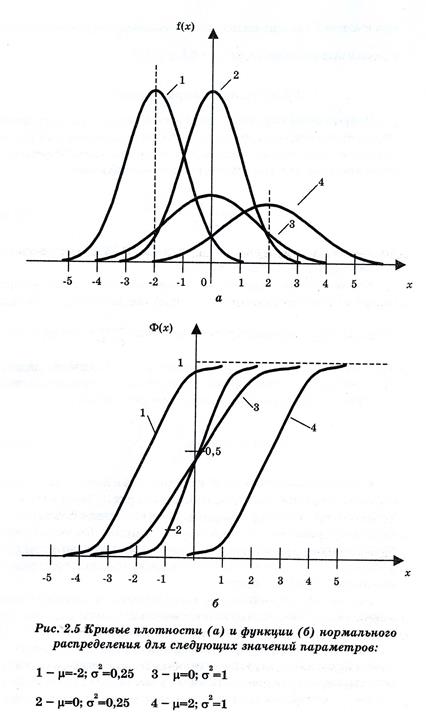
Влияние параметров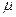 
и 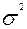на плотность и функцию нормального распределения можно проследить на рис. 2.5. С ростом величины математического ожидания 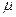обе функции сдвигаются параллельно вправо, не изменяя своей формы. С уменьшением дисперсии 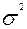кривая плотности распределения вытягивается вверх и одновременно сжимается с боков, а кривая функции распределения становится более крутой.
Так как плотность нормального распределения одномодальна и симметрична относительно математического ожидания 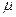, то и 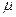одновременно является медианой и единственной модой, т. е. 
.
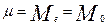Нормальному распределению подчиняются многие встречающиеся на практике случайные величины, образованные в результате суммирования большого числа независимых (или слабо зависимых) случайных величин, подчиненных различным законам распределения.
Если ни одна из этих случайных величин не превалирует над всеми другими, то особенности их распределения в сумме большого числа слагаемых нивелируются и сумма оказывается подчиненной закону, близкому к нормальному закону распределения. Вследствие этого нормальное распределение служит приемлемой моделью для многих физических явлений. В качестве примера отметим, что нормальному распределению подчинены:
-случайные ошибки измерений;
-отклонения параметров изделий (размер, масса, толщина покрытия и др.) от среднего значения в серийном производстве;
-стабильность технологических процессов.
