Дискретная случайная величина Х с возможными значениями 0, 1, …m,…M имеет гипергеометрическое распределение с параметрами n, N, и М,если вероятность того, что она примет значение, равное m, определяется соотношением:

Р(m) = 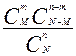, (2.38)

где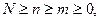

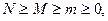
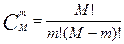- число сочетаний из М по m.

Гипергеометрическое распределение типично для выборочного контроля качества продукции по альтернативному признаку. В этом случае генеральной совокупностью является контролируемая партия продукции объемом N, в которой М единиц продукции несоответствующие. Если из этой партии продукции берется безвозвратная выборка объемом n, то количество несоответствующих изделий в выборке является дискретной случайной величиной, подчиняющейся гипергеометрическому закону распределения. Таким образом вероятность того, что в выборке объемом nбудет обнаружено ровно mнесоответствующих изделий, определяется соотношением (2.38).

На практике для упрощения расчетов по формуле (2.38) можно использовать рекуррентные соотношения [71,87]:

Р(m + 1) = Р(m) ,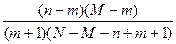

Р(m – 1) = Р(m) , (2.39)

При использовании рекуррентных соотношений для уменьшения погрешности округления сначала вычисляют Р(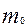 ), а затем применяют как восходящую рекурсию для m > 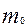, так и убывающую – для m< .

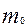Приведем без доказательства выражение для параметров гипергеометрического распределения:

математическое ожидание М(Х) = ;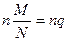

дисперсия .

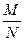Если , в то время как n и q = остаются фиксированными, то гипергеометрическое распределение стремится к биномиальному распределению. Это объясняется тем, что бесповторная выборка мало отличается от повторной выборки, если соотношение мало. Аппроксимация биномиальным распределением применима при условии < 0,1, и вместо выражения (2.38) можно использовать соотношение (2.40).