Биномиальное распределение

Дискретная случайная величина Х распределена по биномиальному закону, если ее возможные значения 0, 1, 2, …m,…n, а вероятность появления таких значений определяется соотношением:

Р(m) = , (2.40)

где .

Например, производится n последовательных независимых опытов, в каждом из которых вероятность осуществления события А постоянна и равна q. Тогда вероятность того, что событие А произойдет точно m раз (если не учитывается порядок осуществления событий) определяется соотношением (2.40).

Применительно к выборочному контролю качества продукции по альтернативному признаку биномиальному распределению подчиняется количество несоответствующих единиц продукции (m) в повторных выборках объемом n, взятых из контролируемой партии продукции с уровнем несоответствия, равным q.

Для биномиального распределения математическое ожидание равно nq, а дисперсия – nq(1 - q).

Для упрощения расчетов по формуле (2.40) удобно использовать следующие рекуррентные соотношения [71,87]:

Р(m + 1) = Р(m) ,

Р(m – 1) = Р(m) (2.41)

Биномиальное распределение при 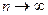стремится к нормальному распределению с математическим ожиданием nq и дисперсией nq(1-q). Это приближение применяется при .