Дискретная случайная величина Х распределена по закону Пуассона, если ее возможные значения 0, 1, 2,…m,…n, а вероятность появления таких значений определяется соотношением:
Р(m) =  , (2.42)
, (2.42)
где  -некоторая положительная величина, называемая параметром распределения Пуассона.
-некоторая положительная величина, называемая параметром распределения Пуассона.
Распределению Пуассона подчиняется количество случайных событий, которые появляются в фиксированные промежутки времени или в фиксированной области пространства, например, количество несоответствий в выборке или количество несоответствий, приходящихся на единицу продукции.
При  <1 значение P(m) монотонно убывает с ростом m, а при
<1 значение P(m) монотонно убывает с ростом m, а при  >1 значение Р(m) с ростом m проходит через максимум вблизи
>1 значение Р(m) с ростом m проходит через максимум вблизи  . Особенностью распределения Пуассона является равенство дисперсии математическому ожиданию М[Х] =
. Особенностью распределения Пуассона является равенство дисперсии математическому ожиданию М[Х] =  .
.
Эта особенность распределения Пуассона позволяет на практике утверждать, что экспериментально полученное распределение случайной величины подчинено распределению Пуассона, если выборочные значения математического ожидания и дисперсии примерно равны.
Для вычисления распределения Пуассона можно пользоваться следующими рекуррентными соотношениями [71,87]:
Р(m + 1) = Р(m)  , Р(m – 1) = Р(m)
, Р(m – 1) = Р(m)  (2.43)
(2.43)
Распределение Пуассона играет важную роль в статистических методах обеспечения качества, поскольку с его помощью можно аппроксимировать гипергеометрическое и биномиальное распределения. Такая аппроксимация допустима, когда  ,
, 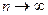 и
и  при условии, что qn имеет конечный предел и q<0,1.
при условии, что qn имеет конечный предел и q<0,1.
Таким образом, в статистических методах обеспечения качества гипергеометрический закон применим для выборок любого объема n и любого уровня несоответствий q, а биномиальный закон и закон Пуассона являются его частными случаями соответственно при условии, если  <0,1 и
<0,1 и 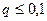 .
.
 2015-10-22
2015-10-22 1519
1519
