Контрольный тест по разделу 1

1. Вычислить и определить погрешность результата , где .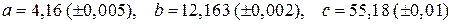

2. Построить интерполяционный полином третьей степени для функции, заданной таблицей. Найти приближённое значение функции при с помощью полученного полинома.

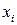
	1,50	1,70	1,90	2,10
	0,6915	0,7580	0,8159	0,8643

3. Отделить вещественный корень уравнения и найти его приближённое значение.

4. Вычислить приближённо определённый интеграл за шесть шагов методом Симпсона и оценить погрешность вычисления.

5. Проинтегрировать методом Эйлера уравнение с начальным условием на отрезке с шагом .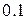

4.4.2. Контрольный тест по разделу 2

1. Найти к.ч. из уравнения .

2. Найти вещественную и мнимую части функции .

3. Найти производную функции .

4. Дана вещественная часть дифференцируемой функции . Восстановить эту функцию.

5. Вычислить 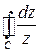, где – граница области .

6. Вычислить интеграл 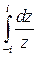вдоль дуги параболы .

7. Разложить в ряд Лорана по степеням функцию .

8. Найти особые точки и определить их тип (для полюсов указать порядок) функции .

9. Найти вычет относительно особых точек функции .

10. Вычислить интеграл .