Международный консорциум «Электронный университет»
Московский государственный университет экономики,
Статистики и информатики
Евразийский открытый институт
Э.Л. Балюкевич
Л.Ф. Ковалева
А.Н. Романников
Дискретная
математика
Учебно-практическое пособие
 Москва 2009
Москва 2009
УДК – 519.1
ББК – 22.176
К – 56
Балюкевич Э.Л., Ковалева Л.Ф., Романников А.Н. ДИСКРЕТНАЯ МАТЕМАТИКА: Учебно-практическое пособие –М.: Изд. центр ЕАОИ, 2009. – 173 с.
ISBN 5–7764–0252–2 © Балюкевич Э.Л., 2009
© Ковалева Л.Ф., 2009
© Романников А.Н. 2009
© Оформление. АНО «Евразийский
открытый институт», 2009
Содержание
Сведения об авторах................................................................... 5
Цели и задачи дисциплины и её место
в учебном процессе..................................................................... 7
Введение........................................................................................ 9
1. Множества............................................................................... 10
1.1. Операции над множествами. Мощность множеств.
Отображение множеств........................................................ 10
1.2. Отношения на множествах.................................................. 27
Тест................................................................................................ 33
2. Математическая логика....................................................... 39
2.1. Алгебра высказываний........................................................ 39
2.2. Проблемы разрешимости. Нормальные формы.............. 56
2.3. Исчисление высказываний.................................................. 73
2.4. Логика предикатов............................................................... 80
Тест................................................................................................ 85
3. Теория графов........................................................................ 96
3.1. Графы..................................................................................... 96
3.2. Деревья................................................................................. 121
3.3. Экстремальные задачи на графах................................... 128
Вопросы для самопроверки...................................................... 140
Контрольные задания............................................................ 142
Контрольное задание №1......................................................... 142
Контрольное задание №2......................................................... 142
Контрольное задание №3......................................................... 145
Контрольное задание №4......................................................... 145
Контрольное задание №5......................................................... 146
Контрольное задание №6......................................................... 147
Контрольное задание №7......................................................... 150
Контрольное задание №8......................................................... 151
Контрольное задание №9......................................................... 152
Контрольное задание №10....................................................... 152
Контрольное задание №11....................................................... 152
Контрольное задание №12....................................................... 155
Контрольное задание №13....................................................... 156
Контрольное задание №14....................................................... 159
Контрольное задание №15....................................................... 162
Список рекомендуемой литературы.................................. 167
Руководство по изучению дисциплины............................. 168
Тема 1. Множества..................................................................... 168
Тема 2. Математическая логика.............................................. 169
Тема 3. Теория графов.............................................................. 171
 Сведения об авторах
Сведения об авторах
Балюкевич Эдуард Людвигович, к.э.н., с.н.с., профессор кафедры прикладной математики МГУЭСИ.
Перечень работ по данной дисциплине, изданных автором:
1. Балюкевич Э.Л. (в соавторстве) Дискретный анализ: учебное пособие. – М.: МЭСИ, 1980. 5,5 п/л.
2. Балюкевич Э.Л. Математические методы в проектировании АСУ. – М.: МЭСИ, 1984, 3 п/л.
3. Балюкевич Э.Л. (в соавторстве) Сборник задач по курсу «Дискретный анализ»: учебное пособие. – М.: МЭСИ, 1987, 4,1 п/л.
4. Балюкевич Э.Л. (в соавторстве) Методические указания к выполнению курсовой работы по курсу «Дискретный анализ». – М.: МЭСИ, 1991, 1 п/л.
5. Балюкевич Э.Л. (в соавторстве) Дискретная математика: учебное пособие. – М.: МГУЭСИ, 2003. 16 п/л.
6. Балюкевич Э.Л. Учебно-практическое пособие. – М.: МГУЭСИ, 2009, 10 п/л (электронная версия).
Ковалева Лидия Федоровна к.т.н., доцент.
Перечень работ по данной дисциплине, изданных автором:
1. Ковалева, Л.Ф. Дискретная математика. – ч. I. – М.: МЭСИ, 2000 (электронное).
2. Ковалева, Л.Ф. (в соавторстве). Дискретная математика. – М.: МЭСИ, 1988.
3. Ковалева, Л.Ф. Применение дискретной математики в экономических задачах. – М.: МЭСИ, 1979.
4. Ковалева, Л.Ф. (в соавторстве). Применение теории графов в экономических задачах. – М.: МЭСИ, 1977.
5. Ковалева, Л.Ф. Математическая логика и теория графов. – ч. I, II. – М.: МЭСИ, 1976, 1977.
6. Ковалева, Л.Ф. (в соавторстве) Дискретный анализ. – М.: МЭСИ, 1980.
7. Ковалева, Л.Ф. Методические указания и контрольные работы по курсу «Дискретная математика» (специальность – «информатика», заочная форма обучения). – М.: МЭСИ, 1998.
8. Ковалева, Л.Ф Методические указания по изучению курса «Дискретная математика» с упражнениями. Задачник. – М.: МЭСИ, 1986.
9. Ковалева, Л.Ф. (в соавторстве). Методические указания и контрольные задания по курсу «Дискретный анализ» для студентов заочного обучения, специальность – экономическая кибернетика. – М.: МЭСИ, 1992.
10. Ковалева, Л.Ф. (в соавторстве). Методические указания по изучению курса «Дискретная математика» (с упражнениями), специальность прикладная математика, АСУ. – М.: МЭСИ, 1986.
11. Ковалева, Л.Ф. (в соавторстве). Методические указания по изучению курса «Дискретный анализ» для студентов заочной формы обучения, специальность - механизированная обработка экономической информации. – М.: МЭСИ, 1987.
12. Ковалева, Л.Ф. (в соавторстве). Методические указания к выполнению курсовой работы.
а) по курсу «Дискретный анализ» для студентов специальности – экономическая кибернетика и АСУ (0715). – М.: МЭСИ, 1991, 1989.
б) по курсу «Дискретная математика» для студентов специальности – прикладная математика (0102). – М.: МЭСИ, 1989.
Цели и задачи дисциплины и её место
в учебном процессе
«Дискретная математика» является математической основой курсов, изучающих современные прикладные экономико-математические методы.
Целью изучения данной дисциплины является прочное усвоение студентами теоретических основ дискретной математики, составляющих фундамент ряда математических дисциплин и дисциплин прикладного характера. Содержание курса «Дискретной математики» используется в курсах: «Теория систем и системный анализ», «Информатика и программирование», «Теория вероятностей и математическая статистика», «Исследование операций и методы оптимизации», «Математическое и имитационное моделирование», «Управление проектом».
Задачей дисциплины является формирование у обучающихся следующих компетенций:
– способности при решении профессиональных задач анализировать социально-экономические проблемы и технико-экономические процессы с применением методов системного анализа и математического моделирования;
– способности применять методы анализа прикладной области на концептуальном, математическом, логическом и алгоритмическом уровнях;
– способности применять системный подход и математические методы в формализации решения прикладных задач.
В результате изучения дисциплины студент должен:
Знать:
– принципы использования языка, средств, методов и моделей дискретной математики в дисциплинах, которым её изучение должно предшествовать, а также в проблемах прикладного характера.
Уметь:
– использовать методы дискретной математики, при изучении дисциплин математического, естественнонаучного и профессионального циклов.
Владеть:
– всем арсеналом методов дискретной математики, который необходим для формирования профессиональных компетенций.
Форма активных методов обучения:
использование учебно-методических комплексов и информационно-компьютерных образовательных технологий, включающих оценочные средства для текущего контроля успеваемости и промежуточной аттестации, разработанных в Московском Государственном Университете Экономики, Статистики и Информатики.
Список дисциплин, знание которых необходимо для изучения дискретной математики:
1. Курс школьной математики.
Введение
Данное пособие рассчитано на читателя, впервые знакомящегося с курсом дискретной математики.
В пособии изложены основные понятия теории множеств и алгебры высказываний, простейшего основного раздела математической логики, сведения из теории графов, рассмотрены задачи по определению экстремальных путей на графе, что позволяет решить такие задачи экономического содержания, как построение самого дешевого нефтепровода, определение скорейшего времени завершения проекта и др.
Данное пособие не претендует на исчерпывающую полноту и абсолютную строгость изложенного материала.
 Тема 1.
Тема 1.

Множества
1.1. Операции над множествами.
Мощность множеств.
Отображение множеств
Под множеством понимают совокупность объектов любой природы, обладающих некоторым общим свойством.
Объекты, объединенные одним общим свойством, называют элементами множества и обозначают a, b, c,... x, y, z. Множества обозначают A, B, C,... X, Y, Z. Запись aÎ A означает, что элемент «a» принадлежит множеству А, bÏA означает, что элемент «b» не принадлежит множеству А.
Множество, число элементов которого конечно, называют конечным и бесконечным в противном случае.
Бесконечные множества разделяются на счетные и несчетные. Если элементы бесконечного множества можно пронумеровать с помощью натурального ряда чисел, то оно называется счетным и несчетным в противном случае. Так, множество четных чисел – счетное, множество действительных чисел – несчетное.
Бесконечные и счетные множества называются дискретными множествами.
Дискретная математика – математика дискретных множеств.
Если каждый элемент множества А есть вместе с тем элемент множества В, то множество А называется частью, или подмножеством множества В и обозначается А Í В.
Если А Í В и В Í А, то множества А и В называются равносильными и обозначаются А=В.
Множество, не содержащее ни одного элемента, называется пустым и обозначается V, Æ. Пустое множество считают конечным множеством и подмножеством любого множества.
Любое множество есть подмножество самого себя. Такое подмножество так же, как и пустое, называют несобственными подмножествами в отличие от всех других подмножеств, которые называют собственными.
Пример.
Пусть А={а1, а2, а3}. Подмножества {а1, а2, а3} и V – несобственные подмножества А. Собственные: {а1}, {а2}, {а3}, {а1, а2}, {а1, а3}, {а2, а3}.
Число подмножеств любого конечного множества, содержащего «n» элементов, равно 2n.
Множество всех элементов, которые могут встретиться в данном исследовании, называют универсальным и обозначают «U».
На множествах определены следующие операции.
Объединением, или суммой множеств А и В называется множество С, элементы которого принадлежат хотя бы одному из множеств А или В.
С=АÈВ={ci: ciÎA или ciÎB}.
Пересечением множеств А и В называется множество С, элементы которого принадлежат как множеству А, так и множеству В.
С=АÇВ={ci: ciÎA и ciÎB}.
Дополнением 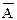 множества А есть множество, элементы которого принадлежат универсальному множеству U и не принадлежат А.
множества А есть множество, элементы которого принадлежат универсальному множеству U и не принадлежат А.
С= 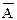 ={ci: ciÎU и ciÏА}.
={ci: ciÎU и ciÏА}.
Данные три основные операции обладают следующими свойствами.
| АÈА=А |  | |
| АÇА=А | ||
| АÈВ=ВÈА | ||
| АÇВ=ВÇА | ||
| (АÈВ)ÈС=АÈ(ВÈС) | ||
| (АÇВ)ÇС=АÇ(ВÇС) | ||
| АÇ(ВÈС)=(АÇВ)È(АÇС) | ||
| АÈ(ВÇС)=(АÈВ)Ç(АÈС) | ||
| AÈU=U | ||
| AÇV=V | ||
| AÇU=A | ||
| AÈV=A | ||
AÈ 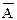 =U =U | ||
AÇ 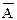 =V =V | ||
 | ||
 | ||
 | ||
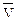 =U =U | ||
 =V =V | ||
AÌ B равносильно 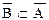 |
Соотношения 1-20 обладают свойствами двойственности: если в одной из формул поменять местами È и Ç, U и V, Ì и É, то получим другую формулу из этого списка.
Порядок выполнения операций:
дополнение (¾ ),
пересечение (Ç),
объединение(È).
Названные операции и свойства к ним могут быть проиллюстрированы диаграммами Эйлера-Венна (рис. 1.1.1).

Рис. 1.1.1
Абстрактная алгебраическая система подмножеств некоторого универсального множества с введенными для них операциями объединения, пересечения, дополнения, обладающая перечисленными выше свойствами, образует Булеву алгебру.
К операциям над множествами относятся также:
1. Разность множеств А\ В – множество, состоящее из элементов множества А и не принадлежащих множеству В.
С=А\ В={ci: ciÎA и ciÏB}
Очевидно, что справедлива формула  =А\ В=
=А\ В=  .
.
2. Симметрическая разность  (А\ В) È (В\ А).
(А\ В) È (В\ А).
Эти операции можно проиллюстрировать на диаграммах Эйлера-Венна (рис. 1.1.2).

Рис. 1.1.2
Декартово (прямое) произведение множеств А и В: А ´ В = С.
3. Декартовым произведением А´В является множество С всех упорядоченных пар <ai,bj>, где aiÎА, bjÎВ, т.е.
С=А´В={<ai,bj>: aiÎА и bjÎВ}.
Иллюстрацией Декартова произведения множеств A={a1,a2}и B={b1,b2,b3} является рис. 1.1.3.

Рис. 1.1.3
В общем случае декартовым произведением множеств А1, А2,... Аn называется множество
А1´А2´... ´Аn={<a1, a2,... an>: a1ÎА1, a2ÎА2... anÎАn}
Рассмотрим несколько упражнений, помогающих усвоить приведенные выше понятия.
Упражнение 1.1.1
Пусть заданы три числовых множества А={2,3,4,10}, В={1,2,10,12}, С={1,9,10}. Требуется указать элементы множеств
| а) AÇBÈBÇC=D, | б) (AÈC) \ (BÇA)=E. |
Множество «D» есть объединение двух множеств AÇB и BÇC, что следует из порядка выполнения действий.
AÇB={2,10}, BÇC={1,10} и D={1,2,10}.
Множество «E» есть разность между объединением AÈC и пересечением BÇA.
AÈC={1,2,3,4,10,12}, BÇA={2,10} и Е={1,3,4,12}.
Упражнение 1.1.2
Пусть множество А состоит из точек M(x,y) плоскости, для которых  , множество В – из точек плоскости, для которых x2+y2£25, С – из точек плоскости, для которых x>0. Требуется изобразить множество AÇB\С.
, множество В – из точек плоскости, для которых x2+y2£25, С – из точек плоскости, для которых x>0. Требуется изобразить множество AÇB\С.
Как следует из условия, множество А есть прямоугольник, В – круг, С – полуплоскость. Решение приведено на рис. 1.1.4.

Рис. 1.1.4
AÇB – «обрезанный» прямоугольник, обведенный на рисунке жирной линией.
AÇB\С – множество точек, полученное удалением из AÇB точек полуплоскости x>0. Результат изображен на рис. 1.1.4 штриховкой.
Упражнение 1.1.3
На диаграмме Эйлера-Венна убедиться в справедливости формул: AÈАÇB=А и (AÈВ)ÇА=А.

Рис. 1.1.5
Данные формулы называют формулами поглощения, т.к. АÇBÌА в первой формуле и АÌ AÈВ во второй.
Формулы поглощения помогают в преобразованиях, упрощающих выражения, задающие некоторые множества.
Упражнение 1.1.4
Упростить выражение
 .
.
В преобразованиях будем пользоваться списком свойств операций над множествами и формулами поглощения. Знак «Ç«в записи формул часто опускают.
S представляет собой произведение двух дополнений. Преобразуем каждое из них. По закону де Моргана имеем
1)  .
.
Затем вновь ко второму сомножителю применяем закон де Моргана, а к первому – свойство 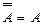 .
.
Получим  .
.
Последний результат получен с использованием формулы поглощения:
 .
.
2)  , так как дважды заменяем разность равносильной формулой
, так как дважды заменяем разность равносильной формулой  . Далее вновь применяем закон де Моргана:
. Далее вновь применяем закон де Моргана:
 .
.
Вынесем за скобки, используя дистрибутивный закон №7,  .
.
 .
.
К выражению, стоящему в скобках, применим дистрибутивный закон №8:

Следовательно, 
Итак, 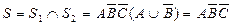 , т.к. по формуле поглощения
, т.к. по формуле поглощения  .
.
Помимо формул поглощения в преобразованиях использовались формулы склеивания  и
и  , одна из которых была доказана в преобразованиях этого упражнения.
, одна из которых была доказана в преобразованиях этого упражнения.
Упражнение 1.1.5
Доказать справедливость следующего равенства и проверить результат на диаграммах Эйлера-Венна.
 .
.
Заменяя разность равносильной формулой, легко приходим к результату:
1)  ,
,
2)  .
.
(Использовали закон де Моргана, дистрибутивный закон №7, закон №14: AÇ 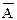 =V, закон №10: VÇA=Æ, закон №12: AÈV=A.)
=V, закон №10: VÇA=Æ, закон №12: AÈV=A.)
Иллюстрируем справедливость этого равенства на диаграммах Эйлера-Венна.

Рис. 1.1.6
Область В\С обведена жирной линией, а область АÇ(В\С) заштрихована  . . | Область АÇВ обведена жирной линией, АÇС – пунктиром, а область (АÇВ)\(АÇС) заштрихована  . . |
Упражнение 1.1.6
Среди 100 деталей прошли обработку на первом станке 42 штуки, на втором – 30 штук, а на третьем – 28. Причем на первом и втором станках обработано 5 деталей, на первом и третьем – 10 деталей, на втором и третьем – 8 деталей, на всех трех станках обработано три детали. Сколько деталей обработано на первом станке и сколько деталей не обработано ни на одном из станков?
В качестве универсального выберем множество всех деталей. Число его элементов равно 100. Пусть А – множество деталей, обработанных на первом станке, В – на втором, С – на третьем. Число элементов множества А обозначим n(A). Оно равно 42, т.е. n(A) = 42. Аналогично, n(В) = 30, n(С) = 28. Обратимся к диаграмме (рис. 1.1.7).

Рис. 1.1.7
Обведенное на чертеже жирной линией множество АÈВÈС есть множество деталей, обработанных хотя бы на одном из станков. Оно разбито на 7 непересекающихся подмножеств, обозначенных на чертеже цифрами. Область 1 есть множество деталей, прошедших обработку на всех трех станках, т.е. множество АÇВÇС. По условию задачи n(АÇВÇС)=3. Множество деталей, обработанных на первом и втором станках, т.е. АÇВ, есть сумма областей, помеченных цифрами 1 и 2. Причем область 2 – множество деталей, обработанных только на первом и втором станках.
По условию задачи n(АÇВ)=5. Следовательно, число деталей, обработанных только на первом и втором станках, равно 5 – 3 = 2. Аналогично, число элементов множества, обозначенного цифрой 3, есть число деталей, прошедших обработку на первом и третьем станках, оно равно n(АÇС) – n (АÇВÇС) =
= 10 – 3 = 7. Число деталей, прошедших обработку только на втором и третьем станках (область 4), равно n(ВÇС) – n(АÇВÇС) = 8 – 3 = 5.
Область, помеченная на чертеже цифрой 5, есть множество деталей, обработанных только на первом станке. Число элементов этого множества получим, если из числа всех обработанных на первом станке деталей вычесть число деталей, обработанных одновременно на первом и втором, а также на первом и третьем станках, в том числе и на всех трех станках 42 - (3 + 2 + 7) = 30.
Аналогично можно определить число деталей, обработанных только на втором станке (область 6), 30 - (3 + 2 + 5) = 20, а также только на третьем (область 7) 28 - (3 + 7 + 5) = 13. Число всех обработанных деталей, т.е. n(АÈВÈС), получим, если сложим число элементов всех областей с 1 по 7. Оно равно 80. Дополнением к нему является множество необработанных деталей U\ АÈВÈС=  , n(
, n( ) = 100 – 80 = 20.
) = 100 – 80 = 20.
Заметим, число элементов непересекающихся множеств А и В (т.е. множеств, для которых выполняется условие АÇВ=V) отличается от числа элементов пересекающихся множеств. Рассмотрим пример.
Упражнение 1.1.7
Лекции по экономике посещают 20 студентов, по математике – 30. Найти число студентов, посещающих лекции по экономике или математике, если 1) лекции проходят в одно и то же время, 2) лекции проходят в разные часы и 10 студентов слушают оба курса.
Очевидно, в первом случае имеем дело с непересекающимися множествами, т.к. студентов, посещающих оба курса, не существует, т.е. АÇВ=V, если А – множество студентов, посещающих лекции по математике, В – по экономике. Следовательно, n(АÇВ)=0, а n(АÈВ)= n(А)+ n(В)=20+30=50.

Рис. 1.1.8
Во втором случае число студентов, посещающих лекции только по математике, – 10, т.к. из 20 человек 10 слушают оба курса. Аналогично только экономику слушают 20 человек из общего числа студентов, равного 30.
Следовательно, лекции по математике или экономике слушают 40 человек, или n(АÈВ) = n(А) + n(В) - n(АÇВ). Графическое решение задачи приведено на рис. 1.1.8.
Эта формула – простейший вариант формулы включений и исключений, отвечающая на вопрос о сумме любого числа пересекающихся множеств n(А1ÈА2È... Аk). Так, для k=3 получим
n(АÈВÈС) = n(А) + n(В) + n(С) – n(АÇВ) – n(АÇС) –
– n(ВÇС) + n(АÇВÇС)
В качестве примера слушателям предлагается получить формулу для k=4.
Если каждому элементу хÎХ поставлен в соответствие некоторый элемент yÎY, то говорят, что определено отображение f множества Х во множество Y. Обозначают y=f(x). Элемент y есть образ элемента х при данном отображении f, х – прообраз элемента y обозначают  .
.
Частным случаем отображения множества Х во множество Y является отображение множества Х на множество Y. Отображение f множества Х в Y является отображением множества Х на Y, если каждому элементу yÎY был поставлен в соответствие какой-либо элемент хÎХ при данном отображении f. Такое соотношение называется сюръективным, т.е. если каждый элемент множества y имеет прообраз, то отображение f сюръективно.
Пусть X={a, b, c, d} Y={2, 4, 6}. Зададим отображения f1 и f2 так:

т.е.

Отображение f1 X в Y является сюръективным, т.е. отображением X на Y, т.к. каждый элемент множества Y имеет прообраз. Отображение f2 несюръективно, элемент «4» не имеет прообраза.
Отображение X в Y называется инъективным, если для каждого элемента yÎY существует не более одного прообраза. Приведенные выше отображения f1 и f2 не являются инъективными.

Отображение f3 – инъективно.
Если отображение f сюръективно и инъективно, оно называется биективным (взаимно однозначное соответствие).
Очевидно, биективное отображение между конечными множествами X и Y возможно только в случае, когда число элементов этих множеств совпадает.
Примером биективного отображения для бесконечных множеств может служить отображение f, установленное между множеством натурального ряда чисел A={1, 2, 3,... n,...} и множеством четных положительных чисел В={2, 4, 6,...} по типу n«2n.

Рис. 1.1.9
На рис. 1.1.9 показана возможность установления биективного отображения между множеством Z точек полуокружности и множеством Х точек открытого отрезка (а, b), а также между множеством Z и множеством Y точек прямой – множеством Y.
z, z1ÎZ; Множества X, Y, Z – несчетные.
x, x1ÎX;
y, y1ÎY.
Упражнение 1.1.8
Установить биективное отображение между множеством
A={1, 6, 11, 16, 21,...} и натуральным рядом чисел.
Очевидно, это можно сделать, поставив в соответствие элементу натурального ряда «n» an=1+5(n-1)ÎA, т.е. n«1+5(n-1).
Упражнение 1.1.9
Установить биективное отображение между множеством точек плоскости и множеством точек сферы, из которой выброшена одна точка.
Очевидно, это можно сделать геометрически (рис. 1.1.10):

Рис. 1.1.10
Обозначим множество точек плоскости Р, множество точек сферы – М, точка А выброшена из сферы, xÎM, yÎP.
Чтобы установить биективное отображение между M и P, достаточно соединить точку В лучом с точкой «х» и получить соответствующую точку «y», или точку В соединить с точкой «y» и получить соответствующую точку «х», т.е. «х»««y».
Два множества называются количественно эквивалентными (или просто эквивалентными), если между ними можно установить биективное отображение.
Исходя из этого определения, можно дать другую формулировку счетного множества: счетным называется множество, эквивалентное натуральному ряду чисел.
Очевидно, что справедливы следующие утверждения:
1. Конечные множества эквивалентны тогда и только тогда, когда они содержат одинаковое число элементов.
2. Два множества, порознь эквивалентные третьему, эквивалентны между собой.
3. Все счетные множества эквивалентны между собой.
4. Всякое множество, эквивалентное счетному множеству, счетно.
О двух эквивалентных множествах говорят, что они имеют одинаковую мощность.
Мощность – это то общее, что есть у эквивалентных множеств. Что общего имеют эквивалентные множества? Общим для них является число элементов. Мощность конечного множества есть число его элементов. Для бесконечных множеств является аналогом количества его элементов.
Все счетные множества имеют мощность, равную мощности натурального ряда чисел. Мощность натурального ряда чисел обозначается  – алеф-нуль.
– алеф-нуль.
Мощность континуума обозначается готической буквой C. Между этими мощностями существует следующая связь:  .
.
Как сравниваются мощности?
Рассмотрим два множества А и В. Если между ними можно установить биективное отображение, то мощности данных множеств равны. Если между множеством А и частью множества В можно установить биективное отображение, а между множеством В и частью А нельзя, то мощность множества А меньше мощности множества В.
Для конечных множеств это положительно очевидно. Для бесконечных множеств оно также справедливо.
Мощность натурального ряда чисел – меньшая среди мощностей всех бесконечных множеств. Следующая по величине – мощность континуума. Пытаясь найти множество, мощность которого была бы промежуточной между мощностями континуума и натурального ряда чисел, Георг Кантор, основатель теории множеств, сформулировал так называемую гипотезу континуума – предложение, отрицающее множество промежуточной мощности. Попытки доказать это предложение привели к серьезным теоретическим исследованиям, связанным с пересмотром оснований математики.
Множества наибольшей мощности не существует, т.к. мощность множества подмножеств исходного множества всегда больше мощности исходного множества.
Упражнение 1.1.10
Доказать, что если А\В эквивалентно В\А, то А и В эквивалентны (рис. 1.1.11).
Решение: А=(А\В)ÈАÇВ
В=(В\А)ÈАÇВ

Рис. 1.1.11
Если (А\В) и (В\А) эквивалентны, то между элементами этих множеств существует биективное отображение. Элементы множества (АÇВ) поставим в соответствие самим себе. Следовательно, между элементами множеств А и В существует биективное отображение, т.е. А и В эквивалентны, т.е. мощности множеств А и В одинаковы.
Сформулируем некоторые основные теоремы, справедливые для счетных множеств.
Теорема 1.Всякая часть счетного множества есть либо конечное, либо счетное множество.
Теорема 2. Сумма конечного или счетного числа конечных или счетных множеств есть счетное множество.
Теорема 3. Всякое бесконечное множество содержит счетное подмножество.
Теорема 4. Если М – несчетное множество, а АÌМ есть конечное или счетное множество, то множества М и М\А эквивалентны.
Теорема 5. Присоединяя к некоторому бесконечному множеству М, счетному или несчетному, счетное или конечное множество А, получим множество МÈА, эквивалентное множеству М.
Теорема 6. Всякое бесконечное множество М содержит часть АÌМ, эквивалентную всему множеству М.
Теорема 7. Множество всех пар натуральных чисел счетно. Под парой натуральных чисел понимают два натуральных числа, расположенных в определенном порядке.
Теорема 8. Множество всех рациональных чисел счетно.
Теорема 9. Множество всех конечных последовательностей, составленных из элементов данного счетного множества, есть счетное множество.
Теорема 10. Множество всех алгебраических чисел счетно.
Теорема 11. Множество континуума несчетно.
Отношения на множествах
Предложения «х – брат y», «x<y» выражают отношения между объектами некоторого множества.
Первое предложение свидетельствует, что два объекта «х» и «y» принадлежат общему классу – сыновья общих родителей. Второе предложение выражает относительный порядок в системе.
Об отношении можно говорить тогда, когда можно выделить множество объектов, на которых это отношение определено.
Приведенные примеры есть бинарные отношения (они выполняются для пары объектов). Тернарные отношения определены для трех объектов, n-арные – для n объектов.
Отношением А на множестве М называют подмножество А множества М´М. Если <x,y> входит в А, то обозначают xAy (<x,y>ÎA). Эта запись читается так: «х находится в отношении А с y».
Итак, отношением называется упорядоченная пара <А,М>, где АÍМ´М, М – множество, на котором определено отношение, А – множество пар, для которых это отношение определено. (Рассматриваем бинарные отношения).
Обратимся к примеру. Зададим отношение «xi – победитель xj» в шахматном турнире из пяти игроков х1, х2, х3, х4, х5, турнир игрался в один круг. Данные приведены в табл. 1.2.1.
Таблица 1.2.1

i ая строка соответствует элементу хi, j ый столбец элементу хj, на их пересечении ставится 1, если отношение хiАхj выполнено, и 0, если нет. Так, единица, стоящая на пересечении 4 ой строки и 1 го столбца, соответствует тому, что игрок х4 выиграл у игрока х1, т.е. <х4Ах1>.
Итак, на множестве М(х1,... х5) отношение «xi – победитель yj» задано матрицей

Такая матрица полностью задает отношение А на множестве М. Прямое произведение М´М представлено двадцатью пятью элементами матрицы (табл. 1.2.1).
Если aijº0 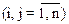 , то имеем пустое отношение, т.е. такое, которое не выполнено ни для какой пары хiхj. Если aijº1, имеем полное отношение, т.е. отношение, выполненное для всех пар. Единичная матрица Е задает диагональное отношение, отношение равенства: <хiАхj>, если хi=хj.
, то имеем пустое отношение, т.е. такое, которое не выполнено ни для какой пары хiхj. Если aijº1, имеем полное отношение, т.е. отношение, выполненное для всех пар. Единичная матрица Е задает диагональное отношение, отношение равенства: <хiАхj>, если хi=хj.
Зададим отношение другим способом, а именно: элементы множества изобразим точками, проведем стрелку от хi к хj, если выполнено хiАхj, получим фигуру – ориентированный граф (рис. 1.2.1).

Рис. 1.2.1
Точки х1, х2, х3, х4, х5 – вершины графа, направленные линии – ребра графа.
Элементы теории графов рассмотрим во второй части данного пособия.
Свойства отношений:
1) Отношение А рефлексивно, если оно выполнено между объектом и им самим, т.е. хАх.
Отношения «быть похожим», «быть знакомым» – рефлексивны. Отношение «быть братом» – нерефлексивно.
2) Если отношение А может выполняться лишь для несовпадающих объектов, то оно антирефлексивно, т.е. из хАу следует, что х¹у.
3) Отношение А называется симметричным, если при выполнении хАу выполнено уАх.
Отношения «быть родственником», «быть похожим на» – симметричны.
4) Отношение А называется асимметричным, если из двух отношений хАу и уАх хотя бы одно не выполнено. Так, приведенный выше пример: отношение «x – победитель y» – асимметрично.
Справедлива теорема: если отношение асимметрично, то оно антирефлексивно.
5) Отношение называется транзитивным, если при выполнении хАу и уАz выполнено хАz.
Примером является отношение «быть больше (меньше)». Так, если х<у и у<z, то х<z.
6) Отношение А называется антисимметричным, если оба соотношения хАу и уАх выполняются только тогда, когда х=у.
Эквивалентность. Отношение эквивалентности определяется отображением множества Х на множество Y и характеризуется разбиением множества Х на классы.
Множество Х разбито на классы, если его можно представить в виде суммы непересекающихся подмножеств:
X=X1ÈX2È... ÈXn,
где XkÌX  и XiÇXj=V (i¹j)
и XiÇXj=V (i¹j) 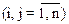 .
.
Так, множество Х учащихся десятых классов некоторой школы разбивается на два класса: Х1 – учащиеся 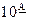 класса, Х2 – учащиеся
класса, Х2 – учащиеся  класса. X=X1ÈX2 и X1ÇX2=V, т.к. нет учеников, обучающихся одновременно и в
класса. X=X1ÈX2 и X1ÇX2=V, т.к. нет учеников, обучающихся одновременно и в 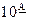 , и в
, и в  классе.
классе.
Два элемента множества Х эквивалентны, если они принадлежат одному и тому же классу.
Каждая пара учащихся 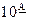 класса – эквивалентные элементы множества Х1 (так же, как и пара
класса – эквивалентные элементы множества Х1 (так же, как и пара  – Х2).
– Х2).
Разбивая множество Х на классы, мы осуществили сюръективное отображение множества всех учащихся Х на множество Y, состоящее из двух элементов у1= 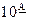 ,у2=
,у2=  . Причем
. Причем  ,
, 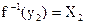 .
.
Другой пример – составление каталога по алфавиту. Множество всех книг в библиотеке Х разбивается на конечное число классов – количество букв алфавита Y. Книги, начинающиеся с одной и той же буквы, принадлежат одному классу, и между любой парой таких книг существует отношение эквивалентности.
В то же время составляя каталог по алфавиту, мы осуществляем сюръективное отображение множества всех книг в библиотеке Х на множество букв алфавита Y.
Отношение эквивалентности – рефлексивно, симметрично и транзитивно. Эти свойства являются необходимыми и достаточными условиями разбиения множества на классы.
Отношение А на множестве М называется толерантностью, если оно рефлексивно и симметрично.
Так, отношение «быть знакомым» соответствует определению толерантности.
Отношение А на множестве Х называется отношением порядка, если оно транзитивно и антирефлексивно.
Отношение порядка характеризует соотношение объектов друг к другу по старшинству, по важности, оно не является симметричным. Отношение x<y на множестве действительных чисел – есть пример отношения порядка.
Множество, на котором задано отношение порядка, называется упорядоченным множеством. Понятие конечного упорядоченного множества совпадает с понятием конечной последовательности, состоящей из различных элементов. Простейшими примерами бесконечных упорядоченных множеств является множество всех целых чисел, множество рациональных чисел.
Заметим, что одно и то же множество можно упорядочить многими различными способами. Так, например, натуральные числа можно упорядочить «естественным образом»: 1, 2, 3, 4,... Это же множество можно упорядочить так, что отдельно нечетные и отдельно четные числа расположены в порядке возрастания, а все нечетные числа считать предшествующими четным, т.е. 1, 3, 5,... 2, 4, 6.
Биективное отображение «f» упорядоченного множества Х на упорядоченное множество Y называют соответствием подобия или подобным соответствием, если оно сохраняет порядок.
Два упорядоченных множества называются подобными, или имеющими один и тот же порядковый тип, если одно из них можно подобно отобразить на другое. Так, два конечных упорядоченных множества Х и Y, состоящих из одного и того же числа элементов, подобны между собой. Указанное выше биективное отображение между всей числовой прямой и интервалом (а,b) является соответствием подобия, и указанные множества подобны (рис. 1.1.9).
Заметим, что подобные множества имеют одну ту же мощность.
Упорядоченное множество называется вполне упорядоченным, если каждое его непустое подмножество содержит первый элемент. Так, все конечные упорядоченные множества – вполне упорядочены. Примером бесконечного вполне упорядоченного множества является множество всех натуральных чисел.
Тест
 2015-10-22
2015-10-22 1082
1082
