2015-10-22
451
1. Вычислите модуль и главное значение аргумента к.ч.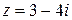 
.
| A. | 5; 53,130 |
| B. | -5; 53,130 |
| C. | 5; -53,130 |
| D. | -5; -53,130 |
2. Выделите вещественную и мнимую части функции 
.
| A. | 
|
| B. | 
|
| C. | 
|
| D. | 
|
3. Вычислите производную функции f(z) в точке 
= i, если f(z) = Sin z.
| A. | 1,543 |
| B. | -1,543 |
| C. | -3,14 |
| D. | 3,14 |
4. Найдите регулярную функцию 
, если известна её мнимая часть 
и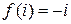 
.
| A. | 
|
| B. | 
|
| C. |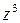 
|
| D. | 
|
5. Вычислите интеграл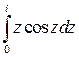 
| A. | 
|
| B. | 
|
| C. | 
|
| D. | 
|
6. Вычислите интеграл 
, где 
– участок параболы 
на отрезке 
.
| A. | 
|
| B. | 
|
| C. | 
|
| D. | 
|
7. Вычислите интеграл 
, где – произвольный замкнутый контур, обходящий точку 
в положительном направлении.
| A. | 
|
| B. | 
|
| C. | 
|
| D. |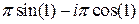 
|
8. Разложите функцию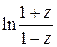 
в степенной ряд 
, используя известное разложение для 
.
| A. | 
|
| B. | 
|
| C. | 
|
| D. |
9. Найдите особые точки функции 
.
| A. |  – полюсы 1-го порядка;  – полюс 2-го порядка;
 – существенно особая точка
|
| B. | – существенно особые точки; – полюс 2-го порядка; – существенно особая точка
|
| C. | – полюсы 1-го порядка; – полюс 2-го порядка;
– полюс 1-го порядка
|
| D. | – полюсы 1-го порядка; – полюс 1-го порядка;
– существенно особая точка
|
10. Вычислите вычеты функции 
относительно точек 
.
| A. |  – полюс 1-го порядка;  – полюс 2-го порядка
|
| B. |  – полюс 1-го порядка; – полюс 2-го порядка
|
| C. |  – полюс 1-го порядка; – полюс 2-го порядка
|
| D. |  – полюс 1-го порядка; – полюс 2-го порядка
|
ОТВЕТЫ
1.C; 2.B; 3.A; 4.A,C; 5.D; 6.B; 7.B; 8.A; 9.A; 10.D
