Система дифференциальных уравнений движения (1) и (2) содержит две неизвестные функции времени 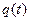 и
и  . Для отыскания стационарного решения этих уравнений воспользуемся методом последовательных приближений. Для этого уравнения запишем в такой форме, чтобы в правых частях стояли только те слагаемые, которые явно содержат
. Для отыскания стационарного решения этих уравнений воспользуемся методом последовательных приближений. Для этого уравнения запишем в такой форме, чтобы в правых частях стояли только те слагаемые, которые явно содержат  , поскольку они вызывают отклонения закона движения от программного (равномерного) вращения.
, поскольку они вызывают отклонения закона движения от программного (равномерного) вращения.
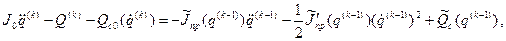
 где волнистой линией обозначены переменные части соответствующих функций.
где волнистой линией обозначены переменные части соответствующих функций.
В нулевом приближении, т.е. при 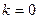 получаем систему уравнений
получаем систему уравнений


Решение этой системы уравнений будем искать в виде
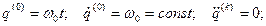

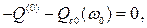 После подстановки получим
После подстановки получим

Поскольку  , а
, а 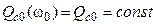 , то определим среднюю угловую скорость входного звена и средний движущий момент
, то определим среднюю угловую скорость входного звена и средний движущий момент


При  получим систему уравнений
получим систему уравнений


Выражение, стоящее в правой части первого уравнения характеризует возмущение, вызывающее отклонение закона движения входного звена (кривошипа) от программного (равномерного) вращения. Возмущающий момент
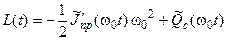 характеризует внутреннюю виброактивность исполнительного механизма.
характеризует внутреннюю виброактивность исполнительного механизма.
Решение системы уравнений в первом приближении (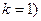 разыскиваем в виде
разыскиваем в виде
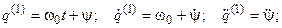

Здесь  - отклонение закона движения входного звена от программного (равномерного) движения, называемое динамической ошибкой по углу;
- отклонение закона движения входного звена от программного (равномерного) движения, называемое динамической ошибкой по углу;  - отклонение движущего момента от среднего значения. Подставив эти решения в систему уравнений, получим
- отклонение движущего момента от среднего значения. Подставив эти решения в систему уравнений, получим

или

Перепишем эти уравнения в операторном виде (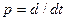 ):
):
 откуда найдем
откуда найдем

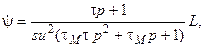
 где
где  - механическая постоянная времени машины.
- механическая постоянная времени машины.
Считаем в MathCad
| Средняя угловая скорость кривошипа |
| Среднее значение приведенного момента инерции |
| Среднее значение приведенного момента сил сопротивления |
| Среднее значение приведенного движущего момента |
| Передаточное отношения редуктора |
| Момент инерции придаточного механизма |
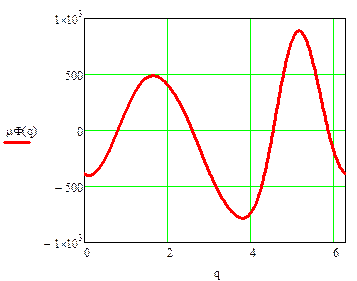
Разложим возмущающий момент на программном движении  в ряд Фурье с точностью до пяти гармоник
в ряд Фурье с точностью до пяти гармоник
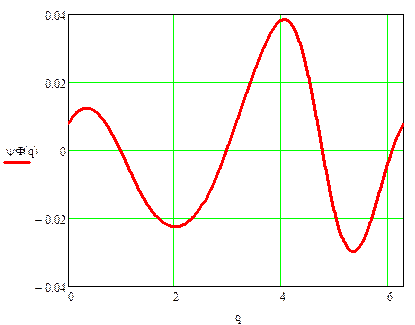
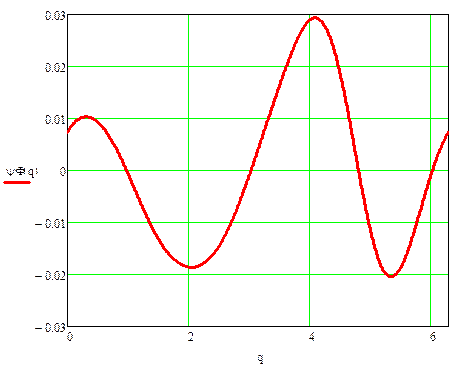
Далее найдем динамическую и статическую ошибку по углу с точностью до пяти гармоник, статическая характеристика не учитывает электромагнитную постоянную времени двигателя:
Динамическая ошибка по углу:
| Динамическая ошибка по скорости: |
| Механическая постоянная времени машины (п е р е с ч е т) |
| Динамическая ошибка по углу (перечсет) |
| Динамическая ошибка по скорости (пересчет) |
Движущий момент с учетом динамической характеристики двигателя
| Переменная часть движущего момента |
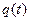 и
и  . Для отыскания стационарного решения этих уравнений воспользуемся методом последовательных приближений. Для этого уравнения запишем в такой форме, чтобы в правых частях стояли только те слагаемые, которые явно содержат
. Для отыскания стационарного решения этих уравнений воспользуемся методом последовательных приближений. Для этого уравнения запишем в такой форме, чтобы в правых частях стояли только те слагаемые, которые явно содержат  , поскольку они вызывают отклонения закона движения от программного (равномерного) вращения.
, поскольку они вызывают отклонения закона движения от программного (равномерного) вращения.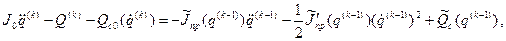
 где волнистой линией обозначены переменные части соответствующих функций.
где волнистой линией обозначены переменные части соответствующих функций.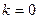 получаем систему уравнений
получаем систему уравнений

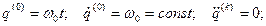

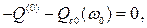 После подстановки получим
После подстановки получим
 , а
, а 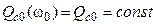 , то определим среднюю угловую скорость входного звена и средний движущий момент
, то определим среднюю угловую скорость входного звена и средний движущий момент

 получим систему уравнений
получим систему уравнений

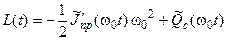 характеризует внутреннюю виброактивность исполнительного механизма.
характеризует внутреннюю виброактивность исполнительного механизма.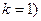 разыскиваем в виде
разыскиваем в виде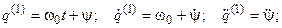

 - отклонение закона движения входного звена от программного (равномерного) движения, называемое динамической ошибкой по углу;
- отклонение закона движения входного звена от программного (равномерного) движения, называемое динамической ошибкой по углу;  - отклонение движущего момента от среднего значения. Подставив эти решения в систему уравнений, получим
- отклонение движущего момента от среднего значения. Подставив эти решения в систему уравнений, получим

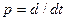 ):
): откуда найдем
откуда найдем
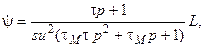
 где
где  - механическая постоянная времени машины.
- механическая постоянная времени машины.


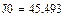



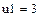

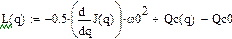

 в ряд Фурье с точностью до пяти гармоник
в ряд Фурье с точностью до пяти гармоник



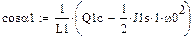
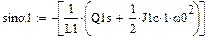


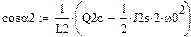


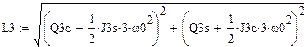


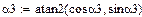

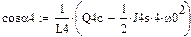










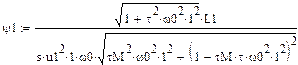

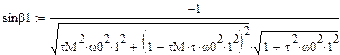

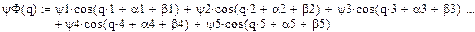

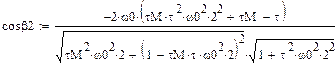








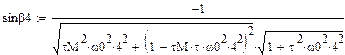
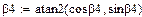


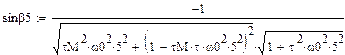

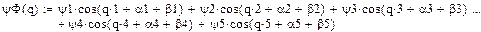


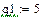




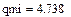











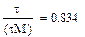

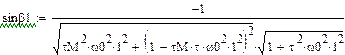








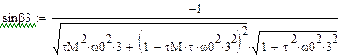
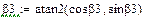


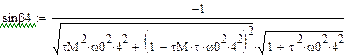









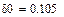


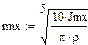




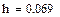




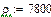

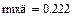






 2017-11-01
2017-11-01 740
740








