2017-11-01
1051
Для RLC- цепи (рисунок 3.1) характеристическое уравнение имеет вид:
,
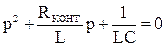корни характеристического уравнения определяются по формуле:
.
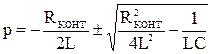Критическое сопротивление RLC- цепи равно: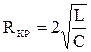 
.
Характер разряда конденсатора зависит от вида корней характеристического уравнения, т.е. от параметров RLC- цепи. Если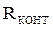 
> RКР, корни характеристического уравнения вещественные и различные, разряд конденсатора апериодический. Если 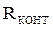= RКР, корни характеристического уравнения вещественные и равные, имеет место предельный случай апериодического разряда конденсатора. Если 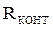< RКР, корни характеристического уравнения комплексно-сопряженные, разряд конденсатора колебательный (рисунок 3.2).
Таким образом, критическое сопротивление контура RКР равно наименьшему сопротивлению контура, при котором разряд конденсатора имеет ещё апериодический характер.
Если в RLC-цепи характер разряда конденсатора колебательный и осциллограмма имеет вид, как на рисунке 3.2, то для экспериментального определения критического сопротивления RКР следует увеличивать сопротивление контура до того значения, пока на осциллограмме не исчезнет последнее колебание и не установится предельный апериодический разряд.
|
|
|
Для колебательного разряда конденсатора коэффициент затухания a (расчетный), частота собственных (свободных) колебаний wСВ (расчетная) определяются по формулам:
.
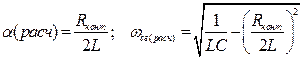Экспериментальные значения a(эксп.) и w св (эксп.) определяются по полученной кривой напряжения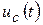 
.
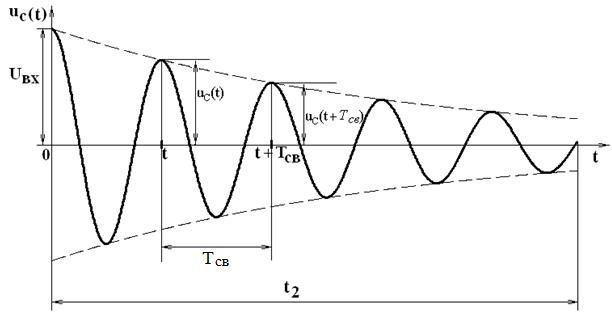
Рисунок 3.2
Частоту свободных колебаний w св (эксп) можно рассчитать по формуле:
,
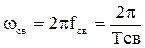где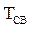 
− период свободных колебаний, определяется по осциллограмме, масштаб по оси времени находится так же, как и в лабораторной работе №1;
t2 − время, в течение которого ЭК замкнут (рисунок 3.2).
Экспериментальное значение a(эксп.) рассчитывается по логарифмическому декременту колебания:
,
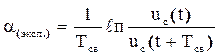где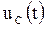 
− напряжение на конденсаторе в момент времени t;
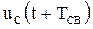− напряжение на конденсаторе в момент времени t+TCB.
