ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Простейшие дифференциальные уравнения в частных производных
Пример. Найти функцию z = z (x, y), удовлетворяющую дифференциальному уравнению
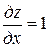 .
.
□ Интегрируя уравнение, получим
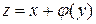 ,
,
где 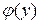 − произвольная функция. Таким образом, функция
− произвольная функция. Таким образом, функция 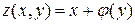 − общее решение заданного дифференциального уравнения. ■
− общее решение заданного дифференциального уравнения. ■
Пример. Решить уравнение
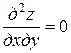 .
.
□ Интегрируя уравнение по х, получим
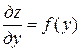 .
.
Проинтегрировав полученный результат по у, находим общее решение
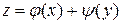 ,
,
где 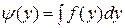 . ■
. ■
Дифференциальные уравнения в частных производных первого порядка
Линейное уравнение
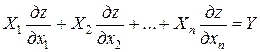 , (1)
, (1)
где z − неизвестная функция независимых переменных 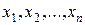 , а функции
, а функции 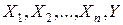 − заданные функции от
− заданные функции от 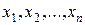 .
.
Если в (1) функции 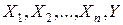 зависят также и от z, то уравнение называется квазилинейным.
зависят также и от z, то уравнение называется квазилинейным.
Если 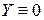 :
:
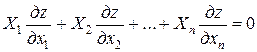 ,
, 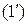
то уравнение называется однородным.
Задача интегрирования линейного однородного уравнения равносильна задаче интегрирования так называемой характеристической системы
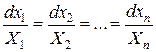 . (2)
. (2)
Пусть решение этой системы определяется равенствами
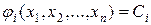
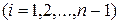 .
.
Тогда общий интеграл дифференциального уравнения 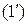 будет иметь вид
будет иметь вид
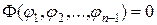 ,
,
где 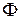 − произвольная непрерывно дифференцируемая функция.
− произвольная непрерывно дифференцируемая функция.
Для интегрирования неоднородного и квазилинейного уравнения (1) строится характеристическая система
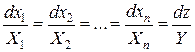 ,
, 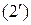
решением которой являются равенства
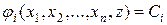
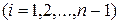 .
.
Тогда общий интеграл дифференциального уравнения 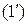 будет иметь вид
будет иметь вид
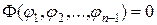 ,
,
где 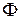 − произвольная непрерывно дифференцируемая функция.
− произвольная непрерывно дифференцируемая функция.
Геометрическая интерпретация. В случае уравнения с двумя независимыми переменными 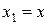 и
и 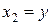 ,
,
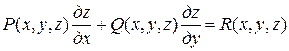 ,
, 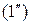
решение 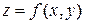 изображается поверхностью в трехмерном пространстве xyz, которая называется интегральной поверхностью этого уравнения.
изображается поверхностью в трехмерном пространстве xyz, которая называется интегральной поверхностью этого уравнения.
Уравнение 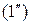 означает, что в каждой точке интегральной поверхности
означает, что в каждой точке интегральной поверхности 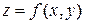 вектор нормали
вектор нормали 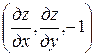 ортогонален заданному в этой точке вектору
ортогонален заданному в этой точке вектору 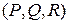 . Система
. Система 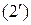 принимает при этом вид
принимает при этом вид
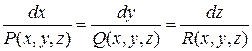 ,
, 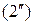
откуда следует, что интегральные кривые этой системы, так называемые характеристики, касательны к векторам 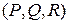 . Поэтому характеристика, имеющая с интегральной поверхностью
. Поэтому характеристика, имеющая с интегральной поверхностью 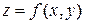 общую точку, целиком лежит на этой поверхности. Через каждую точку пространства проходит интегральная кривая характеристической системы, и интегральные поверхности составляются из характеристик.
общую точку, целиком лежит на этой поверхности. Через каждую точку пространства проходит интегральная кривая характеристической системы, и интегральные поверхности составляются из характеристик.
Пример. Найти общий интеграл уравнения
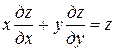 .
.
□ Составим характеристическую систему
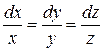 или
или 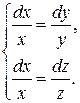
Решая первое уравнение, получим 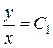 ; решая второе уравнение, получим
; решая второе уравнение, получим 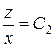 . Теперь можно найти общий интеграл заданного уравнения:
. Теперь можно найти общий интеграл заданного уравнения:
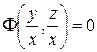 или
или 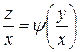 ,
,
т.е. 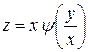 , где
, где 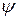 − произвольная функция. ■
− произвольная функция. ■
Пример. Найти поверхность, удовлетворяющую уравнению
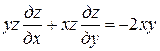
и проходящую через окружность 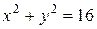 , z = 3.
, z = 3.
□ Построим и решим характеристическую систему
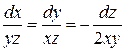 или
или 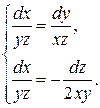 .
.
Освободившись от знаменателя, получим
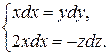 .
.
Интегрируя оба уравнения, получим
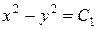 ,
, 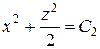 .
.
Общий интеграл заданного уравнения имеет вид
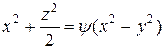 . (*)
. (*)
Из семейства поверхностей, определяемых этим уравнением, нужно выделить поверхность, проходящую через окружность 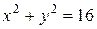 , z = 3. Для того, чтобы найти функцию
, z = 3. Для того, чтобы найти функцию 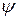 , в равенстве (*) положим
, в равенстве (*) положим 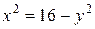 , z = 3. Тогда получим
, z = 3. Тогда получим 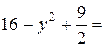
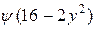 . Пусть
. Пусть 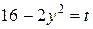 , тогда
, тогда 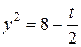 . Следовательно,
. Следовательно, 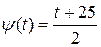 , т.е.
, т.е.
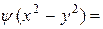
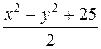 .
.
Подставляя найденное выражение в соотношение (*), получим
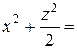
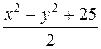 или
или 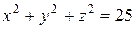 .
.
Таким образом, искомой поверхностью является сфера радиуса R = 5. ■
Дифференциальные уравнения в частных производных второго порядка.
Приведение к каноническому виду
Рассмотрим уравнение второго порядка
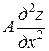 +
+ 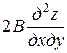 +
+ 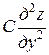 +
+ 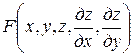 = 0, (1)
= 0, (1)
где А, В, С, z – функции х и у.
Говорят, что уравнение (1) в области D принадлежит гиперболическому типу, если в этой области 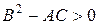 . При
. При 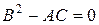 уравнение принадлежит параболическому типу, а при
уравнение принадлежит параболическому типу, а при 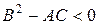 уравнение принадлежит эллиптическому типу.
уравнение принадлежит эллиптическому типу.
Уравнение
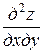 =
= 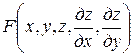
называется каноническим уравнением гиперболического типа;
Уравнение
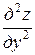 =
= 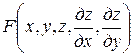
называется каноническим уравнением параболического типа;
Уравнение
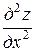 +
+ 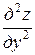 =
= 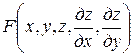
называется каноническим уравнением эллиптического типа.
Дифференциальное равнение
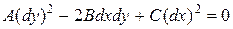
называется уравнением характеристик уравнения (1).
Для уравнения гиперболического типа уравнение характеристик имеет два интеграла: 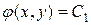 и
и 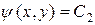 , т.е. существуют два семейства действительных характеристик. С помощью замены переменных
, т.е. существуют два семейства действительных характеристик. С помощью замены переменных 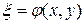 и
и 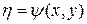 дифференциальное уравнение (1) приводится к каноническому виду.
дифференциальное уравнение (1) приводится к каноническому виду.
Для уравнения параболического типа оба семейства характеристик совпадают, т.е. уравнение характеристик дает лишь один интеграл 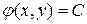 . В этом случае следует сделать замену
. В этом случае следует сделать замену 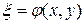 и
и 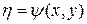 , где
, где 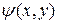 − какая-нибудь функция, для которой
− какая-нибудь функция, для которой 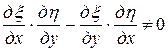 . После такой замены уравнение приводится к каноническому виду.
. После такой замены уравнение приводится к каноническому виду.
Для уравнения эллиптического типа интегралы уравнения характеристик имеют вид 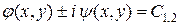 , где
, где 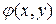 и
и 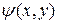 − действительные функции. С помощью подстановки
− действительные функции. С помощью подстановки 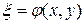 и
и 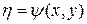 дифференциальное уравнение (1) приводится к каноническому виду.
дифференциальное уравнение (1) приводится к каноническому виду.
Пример. Привести к каноническому виду уравнение
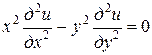 .
.
□ Имеем А = х 2, В = 0, С = 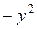 ,
, 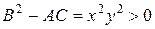 . Следовательно, заданное уравнение является уравнением гиперболического типа.
. Следовательно, заданное уравнение является уравнением гиперболического типа.
Составим уравнение характеристик
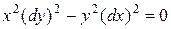 или
или 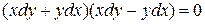 .
.
Получили два дифференциальных уравнения
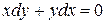 и
и 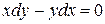 .
.
Решая уравнения, получим
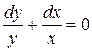 ,
, 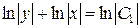 ,
, 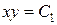 ;
;
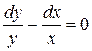 ,
, 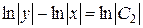 ,
, 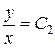 .
.
В результате получили уравнения двух семейств характеристик: 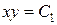 ,
, 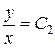 . Введем новые переменные
. Введем новые переменные 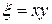 ,
, 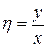 . Выразим частные производные по старым переменным через частные производные по новым переменным:
. Выразим частные производные по старым переменным через частные производные по новым переменным:
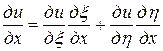 =
=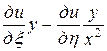 ,
,
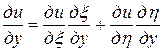 =
=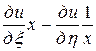 ,
,
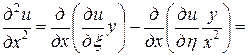
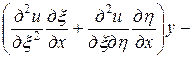
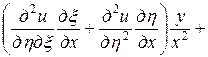
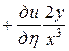 =
= 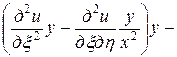
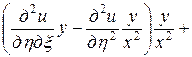
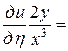
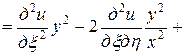
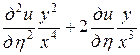 ,
,
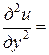
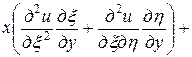
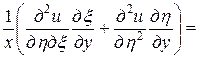
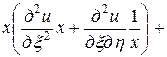
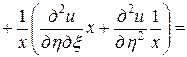
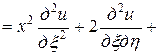
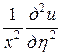 .
.
Подставляя в заданное уравнение найденные выражения вторых производных, получим
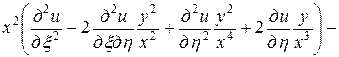
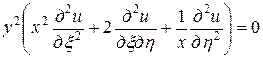 ,
,
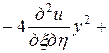
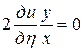 ,
, 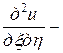
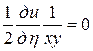 ,
, 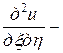
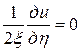 .
.
Окончательный канонический вид заданного дифференциального уравнения
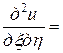
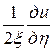 . ■
. ■
Пример. Привести к каноническому виду уравнение
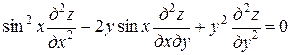 .
.
□ Имеем А = 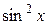 , В =
, В = 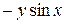 , С =
, С = 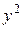 ,
, 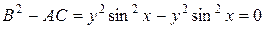 . Следовательно, заданное уравнение является уравнением параболического типа.
. Следовательно, заданное уравнение является уравнением параболического типа.
Уравнение характеристик:
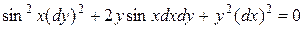 ,
, 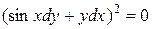
или
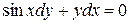 .
.
Разделяя переменные и интегрируя, получим
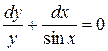 ,
, 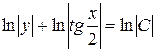 ,
, 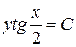 .
.
Замена переменных: 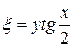 ,
, 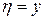 (произвольная функция).
(произвольная функция).
Тогда
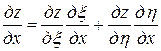 =
=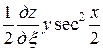 ,
,
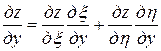 =
=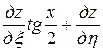 ,
,
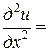
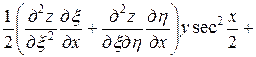
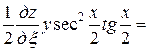
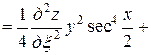
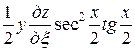 ,
,
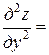
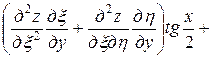
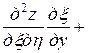
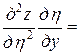
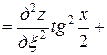
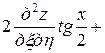
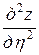 ,
,
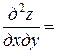
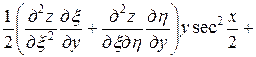
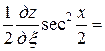
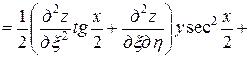
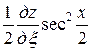 .
.
Подставляя полученные выражения в данное уравнение, получим
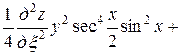
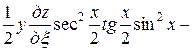
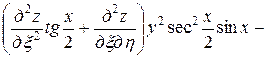
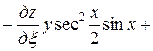
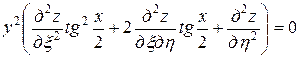 .
.
После упрощения имеем
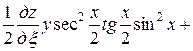
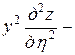
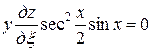 ,
, 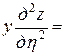
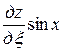 .
.
Так как 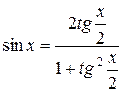 ,
, 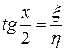 , то
, то 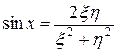 . Окончательно
. Окончательно
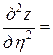
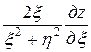 . ■
. ■
Пример. Привести к каноническому виду уравнение
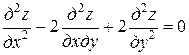 .
.
□ Имеем А = 1, В = −1, С = 2, 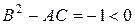 . Следовательно, заданное уравнение является уравнением эллиптического типа.
. Следовательно, заданное уравнение является уравнением эллиптического типа.
Уравнение характеристик:
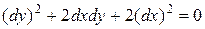 ,
, 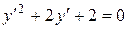 .
.
Отсюда 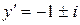 и получаем два семейства мнимых характеристик:
и получаем два семейства мнимых характеристик: 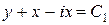 и
и 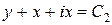 . Замена переменных:
. Замена переменных: 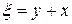 и
и 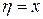 . Тогда
. Тогда
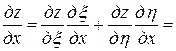
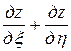 ,
,
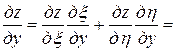
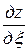 ,
,
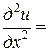
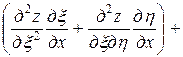
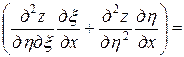
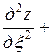
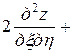
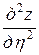 ,
,
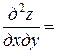
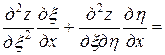
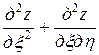 ,
,
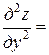
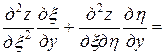
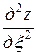 .
.
Подставляя найденные выражения в уравнение, получим
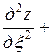
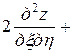
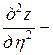
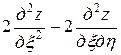
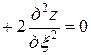
или
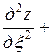
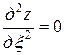 . ■
. ■
 2014-02-09
2014-02-09 1604
1604
