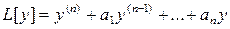 , (1)
, (1)
a1, a2, …, an – постоянные вещевтвенные числа, 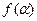 непрерывная в интервале (a,b).
непрерывная в интервале (a,b).
Рассмотрим сначала соответствующие уравнению (1) уравнение 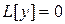 (2),
(2),
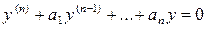 (2)
(2)
Будем искать уравнение (2), следуя Эйлеру, в виде
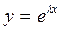 (3),
(3),
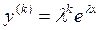 (4)
(4)
Подставляя (4) в уравнение (2), получим
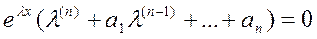 или
или 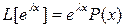 (4)
(4)
Таким образом получаем
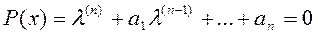 (5)
(5)
– называется характеристическим многочленом или характеристическим уравнением.
Случай 1:
Все корни характеристического многочлена l1, l2, …, ln различны и вещественны.
Каждому корню li соответствует частное решение
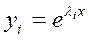 (i=1..n)
(i=1..n)
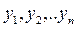 – линейно независимая система функций, т.е. ФСР.
– линейно независимая система функций, т.е. ФСР.
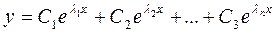 (6) – общее решение уравнения
(6) – общее решение уравнения 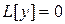 .
.
Пример:
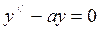 ,
,
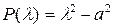 ,
,
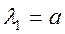
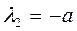
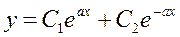 – общее решение данного уравнения.
– общее решение данного уравнения.
Случай 2:
Среди корней характеристического уравнения есть комплексный корень 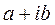
Пусть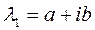 , тогда
, тогда 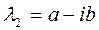 ,
,
l3, l4, …, ln – различные и вещественные корни.
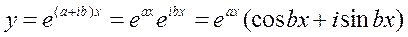 (формула Эйлера)
(формула Эйлера)
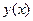 – комплексная функция действительной переменной. Тогда –
– комплексная функция действительной переменной. Тогда –
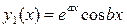 ,
, 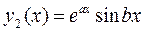 – также
– также
являются решениями уравнения.
Очевидно, что сопряжённый корень не порождает новых решений.
Таким образом, ФСР в данном случае
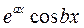 ,
,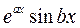 ,
, 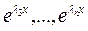
и общее решение имеет вид:
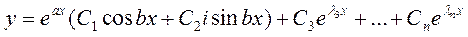
Пример:
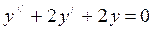 ,
,
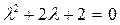 – характеристическое уравнение,
– характеристическое уравнение,
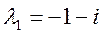
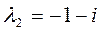
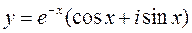 ,
,
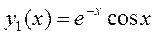 ,
, 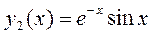 ,
,
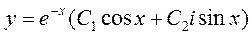 – общее решение.
– общее решение.
Случай 3:
Среди корней характеристического уравнения есть кратный действительный корень.
Пусть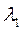 – корень кратности k.
– корень кратности k.
P(λ1) = 0, P/ (λ1)= 0, …, P(k-1) (λ1)=0, P(k) (λ1)≠0.
Запишем полученное ранее выражение 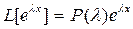 (4) и продифференцируем его по λ m раз, используя для правой части формулу Ньютона-Лейбница, а для левой свойства оператора L.
(4) и продифференцируем его по λ m раз, используя для правой части формулу Ньютона-Лейбница, а для левой свойства оператора L.
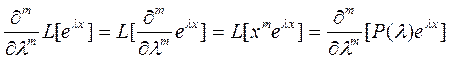 . (9)
. (9)
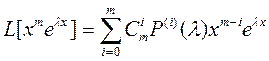 (10)
(10)
Подставим в уравнение (10) λ = λ1 и используем, что
P(λ1) = 0, P/ (λ1)= 0, …, P(k-1) (λ1)=0.
Получим, что
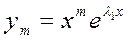 – решение уравнения (10) при m = 0, 1,…, (k-1).
– решение уравнения (10) при m = 0, 1,…, (k-1).
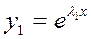 ,
,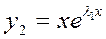 ,…,
,…,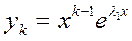 ,
,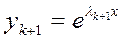 ,…
,…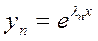 – ФСР.
– ФСР.
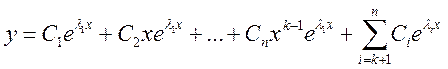 (11)
(11)
(11) – общее решение уравнения (2).
Пример:
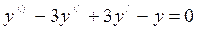 ,
,
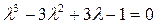 – характеристическое уравнение,
– характеристическое уравнение,
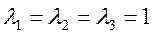
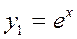 ,
,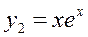 ,
, 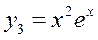 ,
,
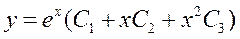 – общее решение.
– общее решение.
Случай 4:
Характеристическое уравнение имеет комплексный корень 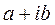 кратности k. Тогда оно имеет и сопряжённый комплексный корень. Таким образом, для построения ФСР нужно 2k линейно независимых решений, соответствующих этим кратным сопряжённым комплексным корням.
кратности k. Тогда оно имеет и сопряжённый комплексный корень. Таким образом, для построения ФСР нужно 2k линейно независимых решений, соответствующих этим кратным сопряжённым комплексным корням.
Отделяя вещественные и мнимые части комплексных решений
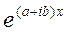 ,
, 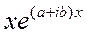 , …,
, …, 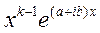 , получим
, получим
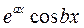 ,
,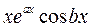 , …,
, …, 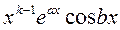
(12)
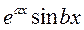 ,
,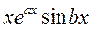 , …,
, …, 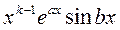 .
.
Таким образом, каждой паре сопряжённых комплексных чисел 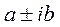 кратности k соответствует 2k линейно независимых решений вида (12).
кратности k соответствует 2k линейно независимых решений вида (12).
И общее решение имеет вид:
|
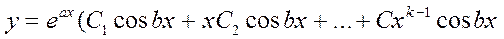
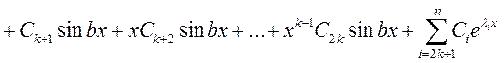
 Пример:
Пример:
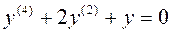
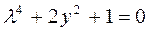
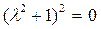
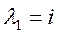
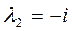
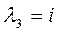
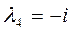
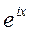 ,
, 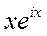 – комплексные решения.
– комплексные решения.
Отделяя вещественные и мнимые части комплексных решений, получим:
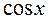
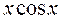
– ФСР
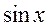
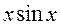
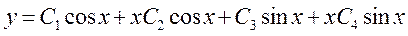 – общее решение данного уравнения.
– общее решение данного уравнения.
13.Нахождение частного решения неоднородного уравнения методом неопределённых коэффициентов.
1.
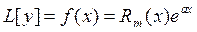 (14), где Rm(x) полином степени m с вещественными или комплексными коэффициентами, а – постоянное вещественное или комплексное или равное нулю число.
(14), где Rm(x) полином степени m с вещественными или комплексными коэффициентами, а – постоянное вещественное или комплексное или равное нулю число.
Случай 1.1:
P(a)≠0
В этом случае частное решение y1 уравнения L[y] = 0 (1) следует искать в виде:
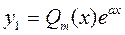 , где
, где 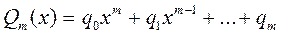 (15)
(15)
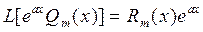 ,
,
где 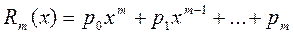 (16)
(16)
Распишем левую часть (16), используя свойства оператора L подробнее
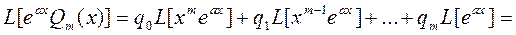
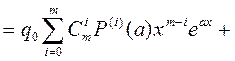
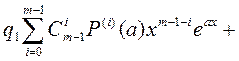
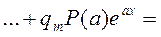
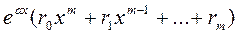 (17)
(17)
Сокращая на 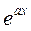 и сравнивая коэффициенты при одинаковых степенях
и сравнивая коэффициенты при одинаковых степенях 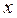 , получаем:
, получаем:
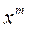 :
: 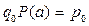
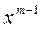 :
: 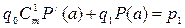
… (18)
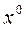 :
: 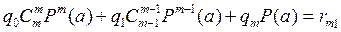
Так как P(a) ≠ 0, все qi находятся из (18) последовательно единственным образом.
Случай 1.2:
«а» является корнем характеристического многочлена кратности k, т.е. P (a) = 0, P/ (a) = 0, …, P(k-1) (a) = 0, P(k) (a) ≠ 0.
Тогда частное решение ищется в виде 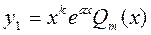 (19)
(19)
Доказательство аналогично случаю 1.
2.
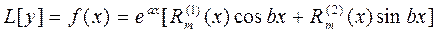 (20)
(20)
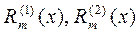 - заданные полиномы от
- заданные полиномы от 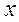 степени равной или меньшей m, причём хоть один из них имеет степень m.
степени равной или меньшей m, причём хоть один из них имеет степень m.
Заменяя 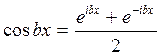 ,
, 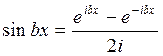 (21)
(21)
2. сводится к случаю 1.
Используем результаты случая 1.
Случай 2.1:
Число 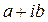 не является корнем характеристического уравнения. Тогда частное решение имеет вид:
не является корнем характеристического уравнения. Тогда частное решение имеет вид:
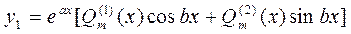 (22)
(22)
где 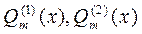 –полиномы степени m с неопределёнными коэффициентами, которые определяются единственным образом.
–полиномы степени m с неопределёнными коэффициентами, которые определяются единственным образом.
Случай 2.2:
Число 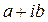 является корнем характеристического уравнения кратности k (k≥1). Тогда частное решение имеет вид:
является корнем характеристического уравнения кратности k (k≥1). Тогда частное решение имеет вид:
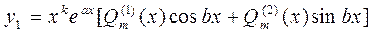 (23)
(23)
где 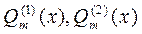 –полиномы степени m с неопределёнными коэффициентами, которые определяются единственным образом.
–полиномы степени m с неопределёнными коэффициентами, которые определяются единственным образом.
Пример 1:
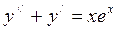 ,
,
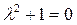 – характеристическое уравнение,
– характеристическое уравнение,
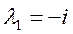
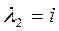
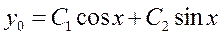 – общее решение однородного уравнения.
– общее решение однородного уравнения.
Случай?.?:
а =1 не является корнем характеристического уравнения. Тогда частное решение имеет вид:
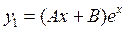 ,
, 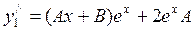
Подставляя значения 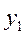 и
и 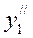 в уравнение и сокращая на e x , получаем:
в уравнение и сокращая на e x , получаем: 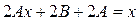 .
.
Откуда 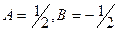 .
. 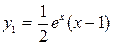 .
.
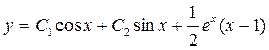 –общее решение данного уравнения.
–общее решение данного уравнения.
Пример:
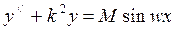 ,
,
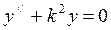 ,
,
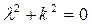 ,
,
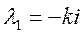
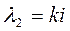
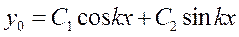 – общее решение однородного уравнения.
– общее решение однородного уравнения.
1) 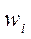 не является корнем характеристического уравнения.
не является корнем характеристического уравнения.
Тогда 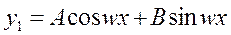
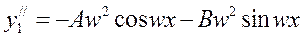
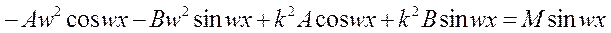
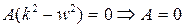
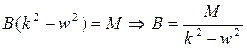
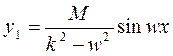
2) 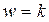 ,
, 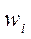 является корнем характеристического уравнения.
является корнем характеристического уравнения.
Тогда 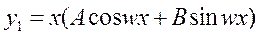
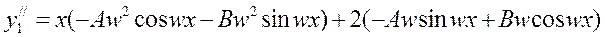 Подставляя значения
Подставляя значения 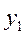 и
и 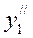 в уравнение , получаем:
в уравнение , получаем:
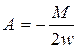 ,
, 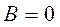
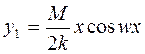 , такой член называется вековым.
, такой член называется вековым.
ЛЕКЦИЯ 5:
 2014-02-10
2014-02-10 1316
1316








