В общем случае дифференциальное уравнение второго порядка можно записать в виде 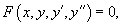 где F − заданная функция указанных аргументов. Если дифференциальное уравнение можно разрешить относительно второй производной y'', то его можно представить в следующем явном виде: где F − заданная функция указанных аргументов. Если дифференциальное уравнение можно разрешить относительно второй производной y'', то его можно представить в следующем явном виде: 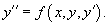 В частных случаях функция f в правой части может содержать лишь одну или две переменных. Такие неполные уравнения включают в себя 5 различных типов: В частных случаях функция f в правой части может содержать лишь одну или две переменных. Такие неполные уравнения включают в себя 5 различных типов: 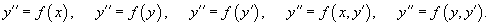 С помощью определенных подстановок эти уравнения можно преобразовать в уравнения первого порядка. В случае произвольных дифференциальных уравнений второго порядка, их порядок можно понизить, если эти уравнения обладают определенной симметрией. Ниже мы обсудим 2 типа таких уравнений (случаи 6 и 7): С помощью определенных подстановок эти уравнения можно преобразовать в уравнения первого порядка. В случае произвольных дифференциальных уравнений второго порядка, их порядок можно понизить, если эти уравнения обладают определенной симметрией. Ниже мы обсудим 2 типа таких уравнений (случаи 6 и 7):
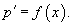 Решая его, находим функцию p (x). Затем решаем второе уравнение Решая его, находим функцию p (x). Затем решаем второе уравнение 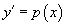 и получаем общее решение исходного уравнения. Случай 2. Уравнение вида y''= f (y) Здесь правая часть уравнения зависит только от переменной y. Вводим новую функцию p (y), полагая y' = p (y). Тогда можно записать: и получаем общее решение исходного уравнения. Случай 2. Уравнение вида y''= f (y) Здесь правая часть уравнения зависит только от переменной y. Вводим новую функцию p (y), полагая y' = p (y). Тогда можно записать: 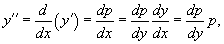 и уравнение принимает вид: и уравнение принимает вид: 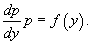 Решая его, находим функцию p (y). Затем находим решение уравнения y' = p (y), то есть функцию y (x). Случай 3. Уравнение вида y''= f (y' ) В данном случае для понижения порядка вводим функцию y' = p (x) и получаем уравнение Решая его, находим функцию p (y). Затем находим решение уравнения y' = p (y), то есть функцию y (x). Случай 3. Уравнение вида y''= f (y' ) В данном случае для понижения порядка вводим функцию y' = p (x) и получаем уравнение 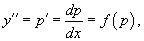 которое является уравнением первого порядка с разделяющимися переменными p и x. Интегрируя, находим функцию p (x) и затем функцию y (x). Случай 4. Уравнение вида y''= f (x,y' ) Используем подстановку y' = p (x), где p (x) − новая неизвестная функция, и получаем уравнение первого порядка которое является уравнением первого порядка с разделяющимися переменными p и x. Интегрируя, находим функцию p (x) и затем функцию y (x). Случай 4. Уравнение вида y''= f (x,y' ) Используем подстановку y' = p (x), где p (x) − новая неизвестная функция, и получаем уравнение первого порядка 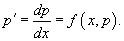 Интегрируя, определяем функцию p (x). Далее решаем еще одно уравнение 1-го порядка Интегрируя, определяем функцию p (x). Далее решаем еще одно уравнение 1-го порядка 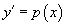 и находим общее решение y (x). Случай 5. Уравнение вида y''= f (y,y' ) Для решения такого уравнения, также как и в случае 2, вводим новую функцию p (y), полагая y' = p (y). Дифференцирование этого равенства по x приводит к уравнению и находим общее решение y (x). Случай 5. Уравнение вида y''= f (y,y' ) Для решения такого уравнения, также как и в случае 2, вводим новую функцию p (y), полагая y' = p (y). Дифференцирование этого равенства по x приводит к уравнению 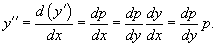 В результате наше исходное уравнение записывается в виде уравнения 1-го порядка В результате наше исходное уравнение записывается в виде уравнения 1-го порядка 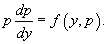 Решая его, находим функцию p (y). Затем решаем еще одно уравнение первого порядка Решая его, находим функцию p (y). Затем решаем еще одно уравнение первого порядка 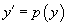 и определяем общее решение y (x). Рассмотренные 5 случаев понижения порядка не являются независимыми. Исходя из структуры уравнений, ясно, что случай 2 следует из случая 5, а случай 3 вытекает из более общего случая 4. Случай 6. Функция F(x, y, y', y'') является однородной функцией аргументов y, y', y'' Если левая часть дифференциального уравнения и определяем общее решение y (x). Рассмотренные 5 случаев понижения порядка не являются независимыми. Исходя из структуры уравнений, ясно, что случай 2 следует из случая 5, а случай 3 вытекает из более общего случая 4. Случай 6. Функция F(x, y, y', y'') является однородной функцией аргументов y, y', y'' Если левая часть дифференциального уравнения 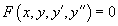 удовлетворяет условию однородности, т.е. для любого k справедливо соотношение удовлетворяет условию однородности, т.е. для любого k справедливо соотношение 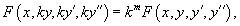 то порядок уравнения можно понизить с помощью подстановки то порядок уравнения можно понизить с помощью подстановки 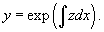 После нахождения функции z (x) исходная функция y (x) находится интегрированием по формуле После нахождения функции z (x) исходная функция y (x) находится интегрированием по формуле 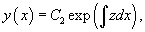 где C 2 − постоянная интегрирования. Случай 7. Функция F(x, y, y', y'') является точной производной Если удается найти такую функцию Ф (x, y, y'), не содержащую второй производной y'' и удовлетворяющую равенству где C 2 − постоянная интегрирования. Случай 7. Функция F(x, y, y', y'') является точной производной Если удается найти такую функцию Ф (x, y, y'), не содержащую второй производной y'' и удовлетворяющую равенству 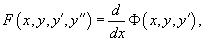 то решение исходного уравнения представляется интегралом то решение исходного уравнения представляется интегралом 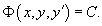 Таким образом уравнение второго порядка можно привести к уравнению первого порядка. В некоторых случаях левую часть исходного уравнения можно преобразовать в точную производную, используя интегрирующий множитель. Таким образом уравнение второго порядка можно привести к уравнению первого порядка. В некоторых случаях левую часть исходного уравнения можно преобразовать в точную производную, используя интегрирующий множитель. |
| Пример 1 |
Решить уравнение y'' = sin x + cos x. Решение. Данный пример относится к случаю 1. Введем функцию y' = p (x). Тогда y'' = p'. Следовательно, 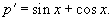 Интегрируя, находим функцию p (x): Интегрируя, находим функцию p (x): 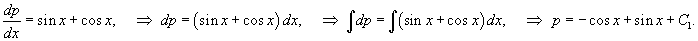 Учитывая, что y' = p (x), проинтегрируем еще одно уравнение 1-го порядка: Учитывая, что y' = p (x), проинтегрируем еще одно уравнение 1-го порядка: 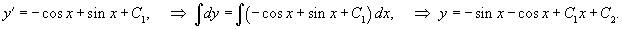 Последняя формула представлят собой общее решение исходного дифференциального уравнения. Последняя формула представлят собой общее решение исходного дифференциального уравнения. |
| Пример 2 |
Решить уравнение 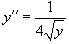 . Решение. Это уравнение относится к типу 2, где правая часть зависит лишь от переменной y. Введем параметр p = y'. Тогда уравнение можно записать в виде . Решение. Это уравнение относится к типу 2, где правая часть зависит лишь от переменной y. Введем параметр p = y'. Тогда уравнение можно записать в виде 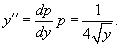 Мы получили уравнение 1-го порядка с разделяющимися переменными для функции p (y). Интегрируем его: Мы получили уравнение 1-го порядка с разделяющимися переменными для функции p (y). Интегрируем его: 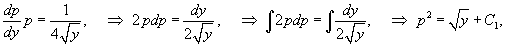 где C 1 − постоянная интегрирования. Извлекая квадратный корень из обеих частей, находим функцию p (y): где C 1 − постоянная интегрирования. Извлекая квадратный корень из обеих частей, находим функцию p (y): 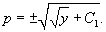 Теперь вспомним, что y' = p и решим еще одно уравнение 1-го порядка: Теперь вспомним, что y' = p и решим еще одно уравнение 1-го порядка: 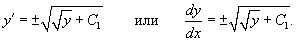 Разделим переменные и проинтегрируем: Разделим переменные и проинтегрируем: 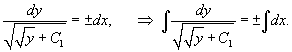 Чтобы вычислить левый интеграл, сделаем замену: Чтобы вычислить левый интеграл, сделаем замену: 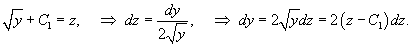 Тогда левый интеграл будет равен Тогда левый интеграл будет равен 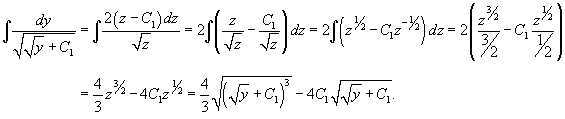 В результате мы получаем следующее алгебраическое уравнение: В результате мы получаем следующее алгебраическое уравнение: 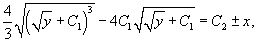 в котором C 1, C 2 являются постоянными интегрирования. Последнее выражение представляет собой общее решение дифференциального уравнения в неявном виде. в котором C 1, C 2 являются постоянными интегрирования. Последнее выражение представляет собой общее решение дифференциального уравнения в неявном виде. |
| Пример 3 |
Решить уравнение 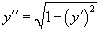 . Решение. Данное уравнение не содержит функции y и независимой переменной x (случай 3). Поэтому полагаем y' = p (x). После этого уравнение принимает вид . Решение. Данное уравнение не содержит функции y и независимой переменной x (случай 3). Поэтому полагаем y' = p (x). После этого уравнение принимает вид 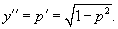 Полученное уравнение первого порядка для функции p (x) является уравнением с разделяющимися переменными и легко интегрируется: Полученное уравнение первого порядка для функции p (x) является уравнением с разделяющимися переменными и легко интегрируется: 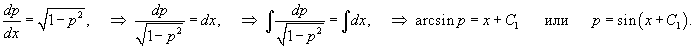 Заменяя p на y', получаем Заменяя p на y', получаем 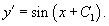 Интегрируя еще раз, находим общее решение исходного дифференциального уравнения: Интегрируя еще раз, находим общее решение исходного дифференциального уравнения: 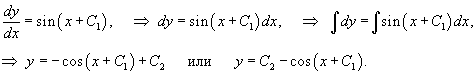 |
| Пример 4 |
Решить уравнение 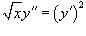 . Решение. В это уравнение не входит явно переменная y, т. е. уравнение относится к типу 4 в нашей классификации. Введем новую переменную y' = p (x). Исходное уравнение преобразуется в уравнение первого порядка: . Решение. В это уравнение не входит явно переменная y, т. е. уравнение относится к типу 4 в нашей классификации. Введем новую переменную y' = p (x). Исходное уравнение преобразуется в уравнение первого порядка: 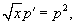 которое решается разделением переменных: которое решается разделением переменных: 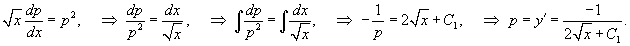 Интегрируя полученное уравнение еще раз, находим функцию y (x): Интегрируя полученное уравнение еще раз, находим функцию y (x): 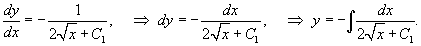 Для вычисления последнего интеграла сделаем замену: x = t 2, dx = 2 tdt. В результате имеем Для вычисления последнего интеграла сделаем замену: x = t 2, dx = 2 tdt. В результате имеем 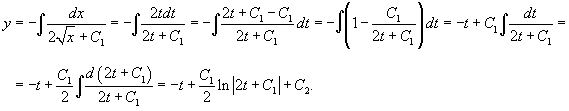 Возвращаясь обратно к переменной x, окончательно получаем Возвращаясь обратно к переменной x, окончательно получаем 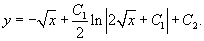 |
| Пример 5 |
Решить уравнение y'' = (2 y + 3)(y')2. Решение. Данное уравнение не содержит явно независимой переменной x, т.е. относится к случаю 5. Пусть y' = p (y). Тогда уравнение запишется в виде 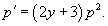 Разделяем переменные и интегрируем: Разделяем переменные и интегрируем: 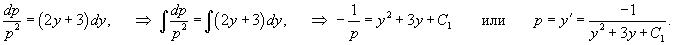 Интегрируя еще раз, получаем окончательное решение в неявном виде: Интегрируя еще раз, получаем окончательное решение в неявном виде: 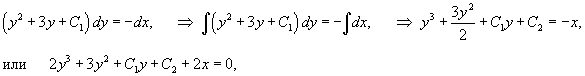 где C 1, C 2 − постоянные интегрирования. где C 1, C 2 − постоянные интегрирования. |
| Пример 6 |
Решить уравнение 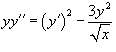 . Решение. Уравнение удовлетворяет условию однородности. Поэтому сделаем следующую замену переменной: . Решение. Уравнение удовлетворяет условию однородности. Поэтому сделаем следующую замену переменной: 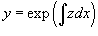 . Производные будут равны . Производные будут равны 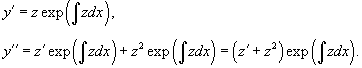 Тогда дифференциальное уравнение принимает вид: Тогда дифференциальное уравнение принимает вид: 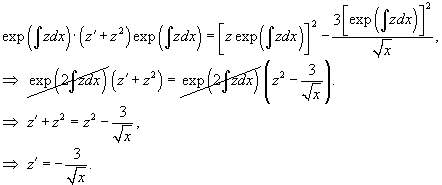 Функция z (x) легко находится: Функция z (x) легко находится: 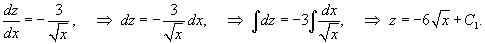 Исходную функцию y (x) определим по формуле Исходную функцию y (x) определим по формуле 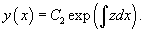 Вычисления приводят к следующему ответу: Вычисления приводят к следующему ответу: 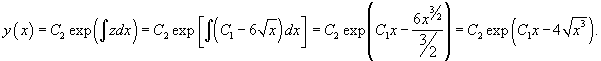 Заметим, что кроме полученного общего решения, дифференциальное уравнение содержит также особое решение y = 0. Заметим, что кроме полученного общего решения, дифференциальное уравнение содержит также особое решение y = 0. |
| Пример 7 |
Решить уравнение yy'' + (y')2 = 2 x + 1. Решение. Можно заметить, что левая часть уравнения представляет собой производную от yy'. Поэтому, обозначая z = yy', получаем следующее дифференциальное уравнение: 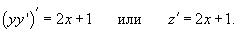 Последнее уравнение легко решается разделением переменных: Последнее уравнение легко решается разделением переменных: 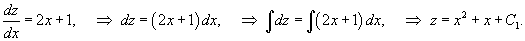 Теперь проинтегрируем еще одно уравнение для y (x): Теперь проинтегрируем еще одно уравнение для y (x): 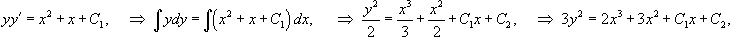 где C 1, C 2 − произвольные постоянные. где C 1, C 2 − произвольные постоянные. |
Линейные дифференциальные уравнения с постоянными коэффициентами. Метод характеристических корней решения линейного однородного уравнения. Нахождение частного решения линейного неоднородного уравнения по виду правой части.
Дифференциальное уравнение вида
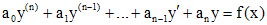 (1)
(1)
где 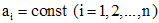 , f - известная функция, называется линейным дифференциальным уравнением n - го порядка с постоянными коэффициентами. Если
, f - известная функция, называется линейным дифференциальным уравнением n - го порядка с постоянными коэффициентами. Если 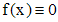 , то уравнение (1) называется однородным, в противном случае - неоднородным. К однородному уравнению, очевидно, применима теорема существования и единственности, причем интервалом определения решений этого уравнения будет вся действительная ось.
, то уравнение (1) называется однородным, в противном случае - неоднородным. К однородному уравнению, очевидно, применима теорема существования и единственности, причем интервалом определения решений этого уравнения будет вся действительная ось.
Если f - непрерывная функция, то общее решение уравнения (1) состоит из суммы общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения (1).
Чтобы решить однородное линейное уравнение с постоянными коэффициентами (1) надо составить характеристическое уравнение
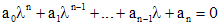 (2)
(2)
и найти его корни 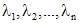 . Каждому простому корню
. Каждому простому корню 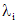 соответствует частое решение однородного уравнения (1), имеющее вид
соответствует частое решение однородного уравнения (1), имеющее вид 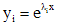 , а каждому корню
, а каждому корню 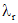 кратности k - решения
кратности k - решения 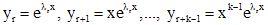 . Произвольная линейная комбинация всех частных решений является общим решением однородного уравнения (1), т.е.
. Произвольная линейная комбинация всех частных решений является общим решением однородного уравнения (1), т.е.
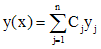 ,
,
где 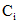 произвольные постоянные.
произвольные постоянные.
Если все коэффициенты однородного уравнения (1) вещественные, то решение можно написать в вещественной форме и в случае комплексных корней 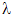 . Для каждой пары комплексно сопряженных корней
. Для каждой пары комплексно сопряженных корней 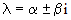 в формулу общего решения включаются слагаемые
в формулу общего решения включаются слагаемые
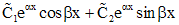 ,
,
если эти корни простые, и слагаемые
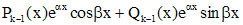 ,
,
если каждый из корней 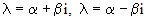 имеет кратность k. Здесь
имеет кратность k. Здесь 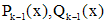 - многочлены степени k-1.
- многочлены степени k-1.
Пример 1. Решить уравнение 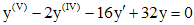 .
.
Решение.
Выпишем характеристическое уравнение, соответствующее данному однородному уравнению
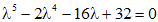 .
.
Разлагая левую часть уравнения на множители, находим корни:
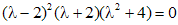 ,
,
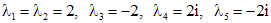 .
.
Следуя выше изложенной теории, выпишем общее решение данного уравнения
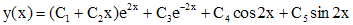 .
.
Для линейных неоднородных уравнений с постоянными коэффициентами и с правой частью специального вида, а именно состоящей из сумм и произведений функций 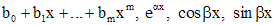 , частное решение можно искать методом неопределенных коэффициентов. Вид частного решения зависит от корней характеристического уравнения. Ниже представлена таблица видов частных решений линейного неоднородного уравнения с правой частью специального вида.
, частное решение можно искать методом неопределенных коэффициентов. Вид частного решения зависит от корней характеристического уравнения. Ниже представлена таблица видов частных решений линейного неоднородного уравнения с правой частью специального вида.
| Правая часть | Число, сравниваемое с корнем характеристического уравнения | Вид частного решения |
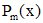 | 0 - не корень | 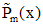 |
| 0 - корень кратности k | 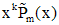 | |
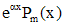 | 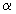 - не корень - не корень | 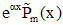 |
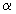 - корень кратности k - корень кратности k | 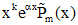 | |
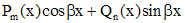 | 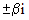 - не корень - не корень | 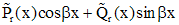 |
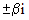 - корень кратности k - корень кратности k | 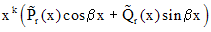 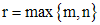 | |
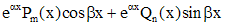 | 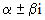 - не корень - не корень | 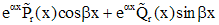 |
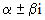 - корень кратности k - корень кратности k | 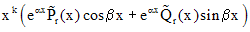 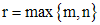 |
Здесь 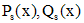 -многочлены степени s, а
-многочлены степени s, а 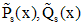 - многочлены степени s, коэффициенты которых нужно найти методом неопределенных коэффициентов. Для того чтобы их найти, нужно функцию, задающую вид частного решения, подставить в исходное дифференциальное уравнение и после приведения подобных слагаемых приравнять соответствующие коэффициенты в правой и левой частях уравнения. В случае, когда для определения вида частного решения нельзя воспользоваться только одной строкой таблицы, применяют принцип суперпозиции.
- многочлены степени s, коэффициенты которых нужно найти методом неопределенных коэффициентов. Для того чтобы их найти, нужно функцию, задающую вид частного решения, подставить в исходное дифференциальное уравнение и после приведения подобных слагаемых приравнять соответствующие коэффициенты в правой и левой частях уравнения. В случае, когда для определения вида частного решения нельзя воспользоваться только одной строкой таблицы, применяют принцип суперпозиции.
Теорема (принцип суперпозиции). Пусть 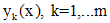 - решения уравнений
- решения уравнений
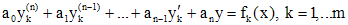 ,
,
соответственно. Тогда
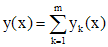
есть решение уравнения
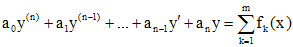 .
.
Пример 2. Решить уравнение 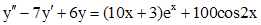 , удовлетворяющее условиям
, удовлетворяющее условиям 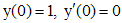 .
.
Решение.
Сначала найдем общее решение данного неоднородного уравнения второго порядка, а затем среди всех решений выберем то, которое удовлетворяет заданным условиям. Так как характеристическое уравнение 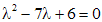 имеет корни
имеет корни 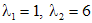 , то общим решением соответствующего однородного уравнения является функция:
, то общим решением соответствующего однородного уравнения является функция:
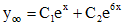 .
.
Правая часть исходного неоднородного уравнения представляет собой сумму двух функций специального вида 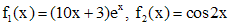 . Найдем методом неопределенных коэффициентов частные решения
. Найдем методом неопределенных коэффициентов частные решения 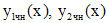 уравнений
уравнений
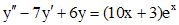 (*)
(*)
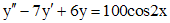 (**)
(**)
соответственно.
Определим частное решение 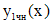 уравнения (*). Правая часть
уравнения (*). Правая часть 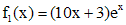 представляет собой произведение многочлена первой степени и
представляет собой произведение многочлена первой степени и 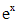 . Число, которое нужно сравнивать с корнем характеристического уравнения - это 1. Оно является простым корнем характеристического уравнения кратности 1. Согласуя с параметрами таблицы, имеем
. Число, которое нужно сравнивать с корнем характеристического уравнения - это 1. Оно является простым корнем характеристического уравнения кратности 1. Согласуя с параметрами таблицы, имеем 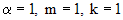 , следовательно, частное решение будем искать в виде:
, следовательно, частное решение будем искать в виде:
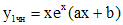 ,
,
где коэффициенты a и b подлежат определению. Подставляя последнее выражение в (*), и приравнивая коэффициенты при одинаковых степенях x в левой и правой частях, получим следующую систему:
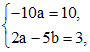
откуда 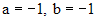 , а значит
, а значит
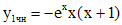 .
.
Правая 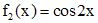 часть уравнения (**) представляет собой произведение многочлена нулевой степени и тригонометрической функции. Число 2i не является корнем характеристического уравнения. Частное решение
часть уравнения (**) представляет собой произведение многочлена нулевой степени и тригонометрической функции. Число 2i не является корнем характеристического уравнения. Частное решение 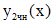 уравнения (**) ищем в виде (
уравнения (**) ищем в виде (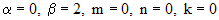 ):
):
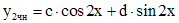 .
.
Подставляя 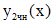 в (**), и приравнивая коэффициенты при sin2x и cos2x справа и слева, получим систему для определения коэффициентов c и d:
в (**), и приравнивая коэффициенты при sin2x и cos2x справа и слева, получим систему для определения коэффициентов c и d:
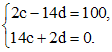
Откуда 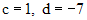 . Поэтому
. Поэтому 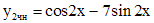 . Согласно принципу суперпозиции, частное решение
. Согласно принципу суперпозиции, частное решение 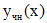 первоначального уравнения имеет вид:
первоначального уравнения имеет вид:
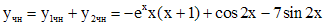 ,
,
а его общее решение определяется функцией:
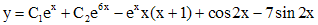 .
.
Чтобы решить задачу Коши, определим значения произвольных постоянных 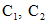 в общем решении. Для этого в решение и его производную подставим x=0. Используя начальные условия
в общем решении. Для этого в решение и его производную подставим x=0. Используя начальные условия 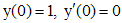 , получим:
, получим:
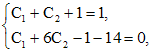
откуда 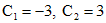 . Значит решение поставленной задачи Коши есть
. Значит решение поставленной задачи Коши есть
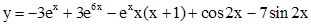 .
.
Линейное неоднородное уравнение (1) с любой правой частью 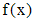 можно решить методом вариации постоянных. Пусть найдено общее решение
можно решить методом вариации постоянных. Пусть найдено общее решение 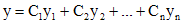 соответствующего линейного однородного уравнения. Тогда решения уравнения (1) ищется в виде
соответствующего линейного однородного уравнения. Тогда решения уравнения (1) ищется в виде
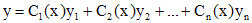 .
.
Функции 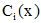 определяются из системы
определяются из системы
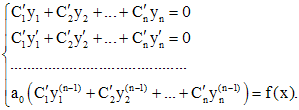
Пример 3. Решить уравнение 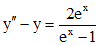 .
.
Решение.
Исходное уравнение есть линейное неоднородное уравнение второго порядка. Решим соответствующее однородное уравнение 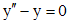 . Характеристическое уравнение для данного однородного уравнения есть
. Характеристическое уравнение для данного однородного уравнения есть 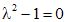 , решениями которого являются
, решениями которого являются 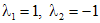 . Тогда общим решением однородного уравнения будет функция
. Тогда общим решением однородного уравнения будет функция 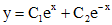 . Тогда решение заданного уравнения будем искать в виде
. Тогда решение заданного уравнения будем искать в виде
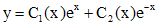 .
.
Функции 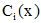 определяются из системы
определяются из системы
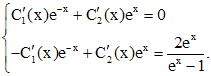
Решая систему, находим
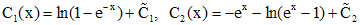 .
.
Тогда функция
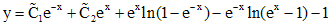
определяет общее решение исходного уравнения.
Рассмотрим дифференциальные уравнения, сводящиеся к линейным уравнения с постоянными коэффициентами.
1. Уравнение Эйлера. Это уравнение вида
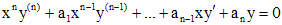 ,
,
где 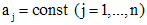 . Заменой
. Заменой 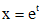 (при
(при  ) уравнение сводится к линейному уравнению с постоянными коэффициентами. На практике решение уравнения Эйлера ищут в виде
) уравнение сводится к линейному уравнению с постоянными коэффициентами. На практике решение уравнения Эйлера ищут в виде 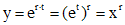 . Для нахождения r получают характеристическое уравнение. Простому корню
. Для нахождения r получают характеристическое уравнение. Простому корню 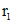 характеристического уравнения соответствует решение
характеристического уравнения соответствует решение 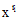 , а m - кратному корню
, а m - кратному корню 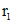 - m линейно независимых решений вида
- m линейно независимых решений вида 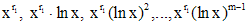 . Если коэффициенты уравнения действительны, а характеристическое уравнение имеет комплексно сопряженные корни
. Если коэффициенты уравнения действительны, а характеристическое уравнение имеет комплексно сопряженные корни 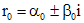 кратности
кратности 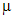 , то уравнение Эйлера имеет
, то уравнение Эйлера имеет 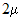 линейно независимых решений вида
линейно независимых решений вида
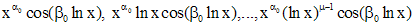 ,
,
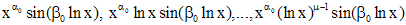 .
.
Пример 4. Решить уравнение 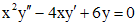 .
.
Решение.
Решение будем искать в виде 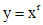 , для нахождения r получаем характеристическое уравнение
, для нахождения r получаем характеристическое уравнение
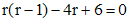 ,
,
решая которое, находим 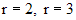 . В итоге получаем общее решение исходного уравнения
. В итоге получаем общее решение исходного уравнения
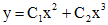 .
.
2. Уравнение Лагранжа. Это уравнение вида
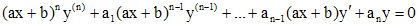 ,
,
где 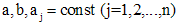 . Заменой
. Заменой 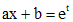 уравнение Лагранжа сводится к линейному уравнению с постоянными коэффициентами.
уравнение Лагранжа сводится к линейному уравнению с постоянными коэффициентами.
Пример 5. Решить уравнение 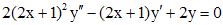 .
.
Решение.
Решение будем искать в виде 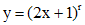 , для нахождения r получаем характеристическое уравнение
, для нахождения r получаем характеристическое уравнение
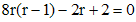 ,
,
решая которое, находим 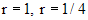 . В итоге получаем общее решение исходного уравнения
. В итоге получаем общее решение исходного уравнения
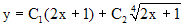 .
.
3. Уравнение Чебышева. Это уравнение вида
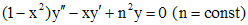 .
.
Заменой 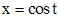 (при
(при 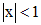 ) уравнение Чебышева сводится к уравнению
) уравнение Чебышева сводится к уравнению
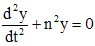 .
.
Пример 6. Решить уравнение 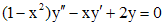 .
.
Решение.
Заменой 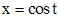 исходное уравнение сводится к
исходное уравнение сводится к
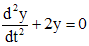 .
.
Решая которое, и переходя к старым переменным получаем общее решение данного уравнения
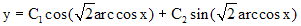 .
.
 2015-01-07
2015-01-07 4533
4533
