Определение. Линейным однородным дифференциальным уравнением n -го порядка с постоянными коэффициентами называется уравнение вида
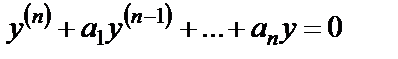 , (30)
, (30)
где 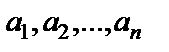 – постоянные.
– постоянные.
Для решения этого уравнения нужно предварительно составить характеристическое уравнение 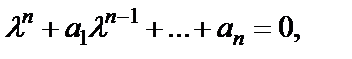 которое получается формально из уравнения (30) заменой производных неизвестной функции на соответствующие степени
которое получается формально из уравнения (30) заменой производных неизвестной функции на соответствующие степени 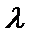 , и найти корни характеристического уравнения
, и найти корни характеристического уравнения 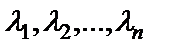 . Рассмотрим линейное однородное дифференциальное уравнение второго порядка
. Рассмотрим линейное однородное дифференциальное уравнение второго порядка
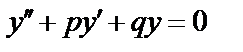 (31)
(31)
Для нахождения общего решения уравнения (31) достаточно знать два линейно независимых частных решения. Для этого составим характеристическое уравнение:
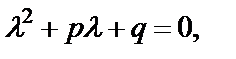 (32)
(32)
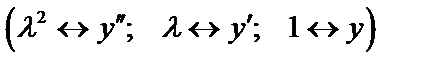
Решим уравнение (32), т.е. найдем 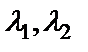 .
.
Возможны случаи:
а) корни характеристичекого уравнения (32) действительные и различные 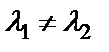 .
.
Общее решение уравнения (31) имеет вид:
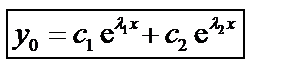 , (33)
, (33)
б) корни характеристического уравнения действительные равные 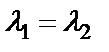 .
.
Общее решение уравнения (31) имеет вид:
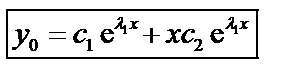 , (34)
, (34)
в) корни характеристического уравнения комплексно сопряженные 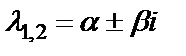 .
.
Общее решение уравнения (31) имеет вид:
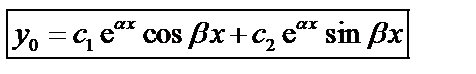 , (35)
, (35)
Примеры. Найти общие решения уравнения:
1. 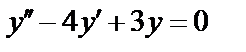
Решение. Составим характеристическое уравнение 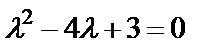 , его корни
, его корни 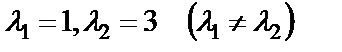 . Следовательно, общее решение данного уравнения будет иметь вид:
. Следовательно, общее решение данного уравнения будет иметь вид: 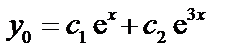 (по формуле 33).
(по формуле 33).
2. 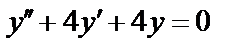
Решение. Характеристическое уравнение: 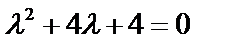 . Это уравнение имеет два равных корня
. Это уравнение имеет два равных корня 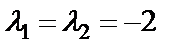 , т.е. –2 – корень второй кратности. Общее решение будет иметь вид:
, т.е. –2 – корень второй кратности. Общее решение будет иметь вид: 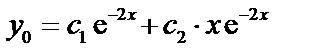 (по формуле 34).
(по формуле 34).
3. 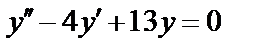
Решение. Характеристическое уравнение: 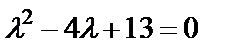 . Корнями этого уравнения будут
. Корнями этого уравнения будут 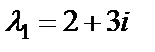 и
и 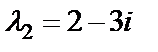 . Общее решение запишется в виде:
. Общее решение запишется в виде: 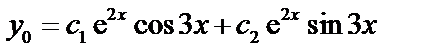 (по формуле 35).
(по формуле 35).
4. 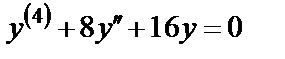
Решение. Характеристическое уравнение: 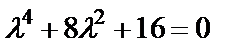 или
или 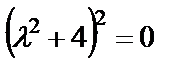 . Находим корни:
. Находим корни: 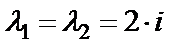 ,
, 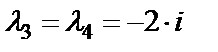 , т.е. характеристическое уравнение имеет пару комплексных сопряженных корней
, т.е. характеристическое уравнение имеет пару комплексных сопряженных корней 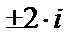 второй кратности. Общее решение будет иметь вид:
второй кратности. Общее решение будет иметь вид: 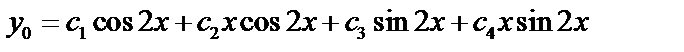 .
.
 2015-05-13
2015-05-13 636
636








