
Пример: Составить уравнение касательной к графику функции  в точке с абсциссой
в точке с абсциссой  .
.
Решение:
1). Найдем производную: 
2). Найдем значение производной в этой точке: 
3). Найдем значение функции в точке 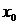
 .
.
4). Теперь подставим все найденные значения в уравнение касательной, получим:

 - уравнение касательной.
- уравнение касательной.
Приближенные вычисления.
Вычислять приближенное значение функции будем по формулам:Формула 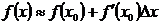 (1)
Пример1: Вычислить приближенное значение функции (1)
Пример1: Вычислить приближенное значение функции  в точке в точке  .
Решение: .
Решение:
 близкая к ней точка близкая к ней точка  .
Найдем: .
Найдем:  .
Найдем .
Найдем  Вычислим
Вычислим  По формуле (1)
По формуле (1)  Пример2: Вычислить приближенное значение функции
Пример2: Вычислить приближенное значение функции  в точке в точке  . .

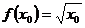 , , 

 По формуле (1) получим:
По формуле (1) получим: 
| Приближенные вычисления.
Формула  (2)
Пример3: Вычислить приближенное значение функции (2)
Пример3: Вычислить приближенное значение функции 
 Пример4: Вычислить приближенное значение функции
Пример4: Вычислить приближенное значение функции 
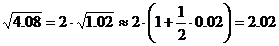 Формула
Формула  (3)
Пример5: Вычислить приближенное значение функции (3)
Пример5: Вычислить приближенное значение функции 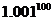
 Пример6: Вычислить приближенное значение функции
Пример6: Вычислить приближенное значение функции 


|
Производная сложной функции.
Задание: найти производную.
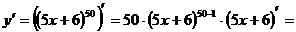




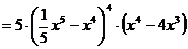
Производная сложной функции
 2017-11-30
2017-11-30 628
628










