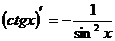Раздел 1. Математический анализ.
Содержание:
1. Задачи, приводящие к понятию производной.
2. Определение производной функции.
4. Геометрический и механический смысл производной.
5. Понятие дифференциала функции, его геометрический смысл.
6. Правила и формулы дифференцирования.
7. Производные элементарных функций.
8. Вторая производная и производные высших порядков.
9. Практическое занятие: Нахождение производных по алгоритму. Вычисление производных сложных функций.
10. Контрольная работа №1.
1. Задачи, приводящие к понятию производной.

Получили неопределённость  - т.е. предел может не существовать, может существовать и при этом быть конечным или бесконечным.
- т.е. предел может не существовать, может существовать и при этом быть конечным или бесконечным.
2. Определение производной функции.

3. Дифференцируемая функция.

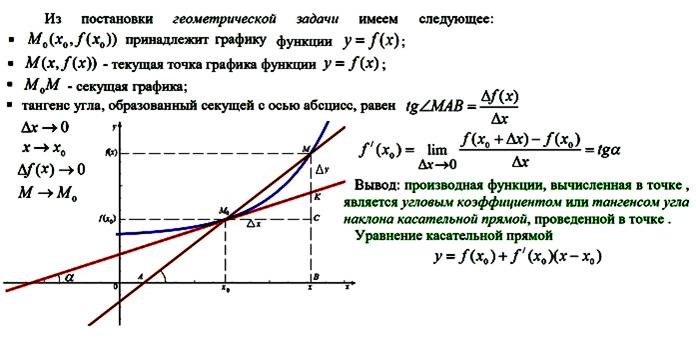
4. Геометрический и механический смысл производной.
Геометрический смысл производной.
Механический смысл производной.

5. Понятие дифференциала функции, его геометрический смысл.
Дифференциалом функции y=f(x) в x0 называется главная, линейная относительно  , часть приращения функции.
, часть приращения функции.
 .
.
Покажем, что  и dy эквивалентные бесконечно малые при
и dy эквивалентные бесконечно малые при  :
:
 (
( бесконечно малая).
бесконечно малая).
 Геометрический смысл дифференциала:
Геометрический смысл дифференциала:
Проведем к графику функции y=f(x) в точку M(x;y) касательную MT и рассмотрим ординату этой касательной для точки  .
.
На рисунке  ,
, 
Из прямоугольного треугольника MAB имеем:  , т.е.
, т.е.  .
.
Но, согласно геометрическому смыслу производной, 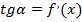 .
.
Поэтому 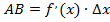 или
или  .
.
Это означает, что дифференциал функции y=f(x) в точке x0 равен приращению ординаты касательной к графику функции в этой точке, когда х получает приращение 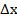 .
.
6. Правила и формулы дифференцирования.
Обозначение производной  , где
, где  – это любая функция.
– это любая функция.
-
 , с – любое число.
, с – любое число.
Пример: 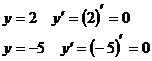
-
 .
.
Пример: 
Число, стоящее перед переменной всегда выносим за скобку и находим производную переменной.
Пример: 
 , т. к. сократим на 4.
, т. к. сократим на 4.

Пример: 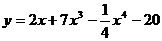

Пример: 
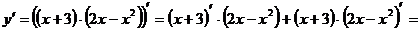
Находим значение производной только там, где стоит знак производной, т.е. штрих.
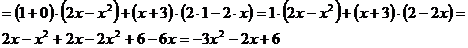
Пример: 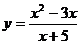

7. Производные элементарных функций.
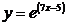



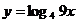



8. Вторая производная и производные высших порядков.
 2017-11-30
2017-11-30 715
715
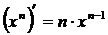
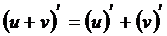
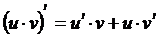

 -
-