координатах – уравнения Лагранжа второго рода

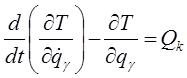
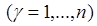. (6.1)

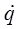– обобщенная скорость

Уравнения (6.1) представляют собой дифференциальные уравнения движения СМТ в обобщенных координатах. Эти уравнения называют уравнениями Лагранжа второгорода.

Запишем теперь уравнения (6.1) для консервативных голономных СМТ. В этом случае обобщенные силы 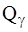могут быть выражены через потенциальную энергию СМТ:

,

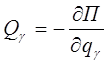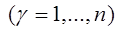
и, следовательно, уравнения примут вид:

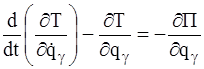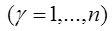, (6.2)

Введем понятие кинетического потенциала (иначе называемого функцией Лагранжа):

L_к = T – П,

тогда уравнения (6.2) можно написать в форме:

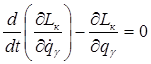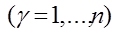. (6.3)

Уравнения (6.3) представляют собой уравнения Лагранжа второго рода для консервативных систем.