Пусть u = u (x) и v = v (x) – непрерывно дифференцируемые функции, тогда 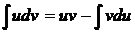 – формула интегрирования по частям (произвольная постоянная интегрирования С здесь включена в слагаемое
– формула интегрирования по частям (произвольная постоянная интегрирования С здесь включена в слагаемое 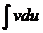 ).
).
Пример 3.5.4. Найти 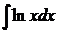 .
.
○ 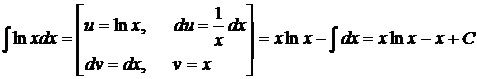 .●
.●
Пример 3.5.5. Найти 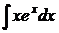 .
.
○ 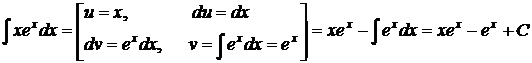 .●
.●
Примечание. Иногда бывает необходимо повторное интегрирование по частям.
Пример 3.5.6. Найти 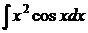 .
.
○
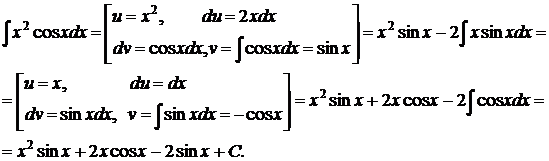 ●
●
Отметим три основных класса функций, интегралы от которых берутся по частям:
| I | 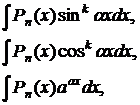 где
где 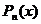 – многочлен n -ой степени, n, k, α ÎN – многочлен n -ой степени, n, k, α ÎN
| 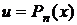
| Интегрирование по частям применять n раз. |
| II | 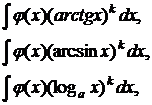
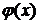 – рациональная или иррациональная функция, в частности, – рациональная или иррациональная функция, в частности, 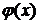 º1. º1.
| 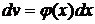
| Интегрирование по частям применять k раз. |
| III | 
| u – любая из функций
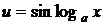
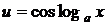
| Применяя двукратное интегрирование по частям получим линейное уравнение, относительно искомого интеграла. Из этого уравнения и находится данный интеграл. |
 2017-11-30
2017-11-30 243
243








