Неправильную рациональную дробь всегда можно свести к правильной, разделив числитель на знаменатель «столбиком» и выделив из дроби целую часть. Поэтому будем рассматривать задачу интегрирования правильной рациональной дроби.
Всякую правильную рациональную дробь можно представить в виде суммы конечного числа следующих видов простейших дробей:
1)  , 2)
, 2) 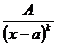 , 3)
, 3)  , 4)
, 4)  , где k и l – целые числа.
, где k и l – целые числа.
Теорема 3.5.3. Для дроби  , знаменатель которой имеет вид
, знаменатель которой имеет вид  , где
, где  , справедливо следующее разложение на сумму простейших дробей:
, справедливо следующее разложение на сумму простейших дробей:

 ,
,
где k и l – целые числа.
Одним из наиболее простых методов определения коэффициентов в разложении правильной дроби на простейшие является метод неопределенных коэффициентов. Рассмотрим его на примере.
Пример 3.5.7. Разложить дробь  на сумму простейших дробей.
на сумму простейших дробей.
○По Теореме 3.5.3 ищем разложение в виде:
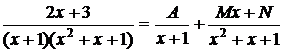
Приводим дроби к общему знаменателю  :
:
 , откуда
, откуда
 .
.
Раскрывая скобки получаем:
 .
.
В правой части уравнения приводим подобные слагаемые (левую оставляем без изменений), получаем
 .
.
Из последнего равенства, приравнивая коэффициенты при одинаковых степенях х в левой и правой его частях, получаем

Отсюда  .●
.●
Пример 3.5.8. Найти  .
.
○ Представим  в виде
в виде  , тогда по теореме 3.5.3:
, тогда по теореме 3.5.3: 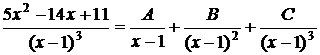 ,
,
 ,
,
 ,
,
 .
.
Приравнивая коэффициенты при одинаковых степенях х в левой и правой частях последнего равенства, получаем

 .
.
Найдем 
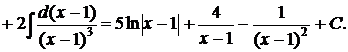 ●
●
 2017-11-30
2017-11-30 214
214








