Моделирование случайных объектов

При математическом представлении реальных объектов случайной природы возникает необходимость моделирования случайных величин, случайных событий и случайных процессов. Формирование на ЭВМ реализаций случайных объектов любой природы сводится к выработке и преобразованию случайных чисел.

Для моделирования случайного события А, вероятность которого равна Р, используется попадание случайного числа r, равномерно распределённого в интервале [0,1], в диапазон вероятностей [0,Р]. В таком случае считают, что событие А наступило, в противном случае – не наступило.

При моделировании дискретных случайных величин наиболее часто используется метод последовательных сравнений. Случайное число r последовательно сравнивают со значением суммы вероятностей

Р ₁ + Р ₂ + …. P_n,

где Р ₁ – вероятность наименьшего значения случайной величины У;

Р ₂ – вероятность второго по величине значения.

При первом выполнении условия r > 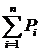проверка прекращается и дискретная случайная величина У считается принявшей значение y_i.

Процесс можно ускорить, применяя методы оптимизации перебора: дихотомии, ранжирования Р и т. д.

Величины Р_i рассчитывают по функциям распределения вероятности, соответствующим моделируемому закону.

При моделировании непрерывных случайных величин чаще всего используется метод, основанный на замене закона распределения непрерывной случайной величины специальным расчётным соотношением, позволяющим вычислять значение случайной величины по значению случайного числа, равномерно распределённого на интервале [0,1]. Такие соотношения получены практически для всех наиболее распространённых видов распределений. В качестве примера приведём расчётные соотношения для двух законов распределения:

- показательного:

х = – ln (r), (12)

где λ – параметр показательного распределения,

r – равномерно распределённое случайное число;

- нормального:

х = m +s ,(13)

где m, s – параметры нормального распределения,

r – равномерно распределённое случайное число.