Параграф 2.7: Прохождение случайных сигналов, через линейные, параметрические и нелинейные системы
Исследования преобразований случайных процессов при их прохождении через непрерывные системы (как с постоянными так и переменными детерминироваными и случайно меняющимися параметрами) связано с решением задач двух типов:
1. по данной корреляционной функции (энергетическому спектру) входного воздействия Х(t) найти корреляционную функцию (энергетический спектр) отклика У(t) на входе непрерывной системы, заданной ее характеристиками.
2. Зная многомерное распределение Х(t) найти многомерные распределения У(t).
Вторая из указанных задач является более общей. Из ее решения очевидно, может быть получено и решение первой задачи, однако первая задача может быть решена и более просто без нахождения многомерных распределений.
Рассмотрим основной подход к определению корреляционной функции отклика линейной системы (параметрической) при случайном входном воздействии.
Произвольный случайный процесс X(t), поступающий на вход системы в общем случае можно представить как сумму центрированного процесса X(t) и его математического ожидания mx(t)
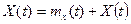 (1)
(1)
Обобщением линейной системы является параметрическая линейная система со случайно изменяющимися параметрами. Ее импульсная характеристика 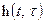 и частотная передаточная функция
и частотная передаточная функция 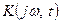 представляет собой нестационарный случайный процесс и по аналогии с (1) так же могут быть представлены в виде сумм математических ожиданий процессов
представляет собой нестационарный случайный процесс и по аналогии с (1) так же могут быть представлены в виде сумм математических ожиданий процессов 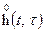 и
и 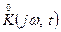 и центрированных процессов.
и центрированных процессов.
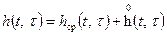 (2)
(2)
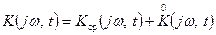 (3)
(3)
Частному случаю параметрической линейной системы с детерминировано изменяющимися параметрами в выражениях (2) и (3) соответствуют
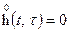 (4)
(4)
и
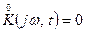 (5)
(5)
а варианту линейной стационарной системы соответствуют
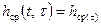 (4)
(4)
и
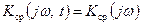 (5)
(5)
Подставляя (1) и (2) в выражение (П*), связывающее отклик y(t) параметрической системы с входным воздействием ее импульсной характеристикой можно убедиться, что отклик обобщенной линейной системы с характеристикой 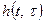 (или
(или 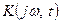 ) на произвольное входное воздействие может быть определен суммой четырех компонентов.
) на произвольное входное воздействие может быть определен суммой четырех компонентов.
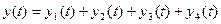 (6)
(6)
где
y1(t) — отклик детерминированной параметрической системы с характеристиками 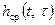 или
или 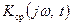 на детерминированное воздействие mx(t).
на детерминированное воздействие mx(t).
y2(t) — отклик детерминированной системы с характеристикой 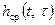 или
или 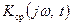 на центрированное случайное воздействие X(t).
на центрированное случайное воздействие X(t).
y3(t) — отклик системы с центрированной характеристикой 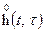 или
или 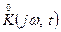 на детерминированное воздействие mx(t).
на детерминированное воздействие mx(t).
y4(t) — отклик системы с центрированной случайной характеристикой 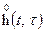 или
или 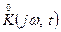 на центрированное случайное воздействие
на центрированное случайное воздействие 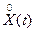 .
.
Поскольку, во-первых, детерминированные и флуктуационные части любого случайного процесса статистически независимы и, во-вторых, в силу линейности связь между входным воздействием и характеристиками системы также отсутствуют можно считать, что слагаемые 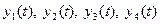 между собой статистически независимы. Это означает, что корреляционная функция или энергетический спектр процесса x(t) могут быть найдены суммированием корреляционных функций или спектров отдельных слагаемых выражения (6).
между собой статистически независимы. Это означает, что корреляционная функция или энергетический спектр процесса x(t) могут быть найдены суммированием корреляционных функций или спектров отдельных слагаемых выражения (6).
Параграф 2.7.2: Определение корреляционной функции отклика y4(t) линейной параметрической системы со случайной характеристикой 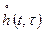 при случайном входном воздействии
при случайном входном воздействии 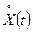
По определению корреляционной функции в этом случае можно записать:
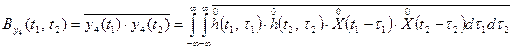 .
.
Поскольку, как отмечалось, характеристика системы 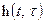 и входной сигнал
и входной сигнал 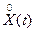 представляют собой независимые процессы, справедливо соотношение
представляют собой независимые процессы, справедливо соотношение
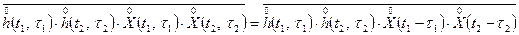 .
.
С учетом этого и, принимая во внимание тот факт 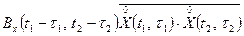 , где Bx() — функция автокорреляции входного сигнала, получаем
, где Bx() — функция автокорреляции входного сигнала, получаем
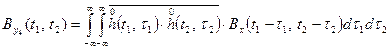 (7)
(7)
Из выражения (7) видно, что корреляционная функция 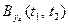 процесса на выходе линейной системы не зависит от распределения входного процесса, а определяется лишь его корреляционной функцией и характеристикой системы.
процесса на выходе линейной системы не зависит от распределения входного процесса, а определяется лишь его корреляционной функцией и характеристикой системы.
Введем новые переменные 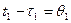 и
и 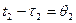 . Тогда
. Тогда
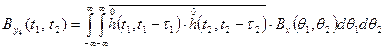 (8)
(8)
При стационарном входном воздействии 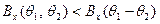 . Подставляя результат в формулу (8), можно увидеть, что на выходе линейной системы с переменными параметрами отклик нестационарен, даже при стационарном входном воздействии (т.к.
. Подставляя результат в формулу (8), можно увидеть, что на выходе линейной системы с переменными параметрами отклик нестационарен, даже при стационарном входном воздействии (т.к. 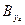 остается при этом функцией двух параметров t1 и t2, а не одного, равного t2 – t1.
остается при этом функцией двух параметров t1 и t2, а не одного, равного t2 – t1.
Воспользовавшись обратным преобразованием Фурье и, проделав необходимые преобразования, можно выразить корреляционную функцию 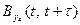 через энергетический спектр входного процесса
через энергетический спектр входного процесса 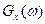 и частотную передаточную функцию
и частотную передаточную функцию 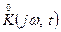 следующим образом:
следующим образом:
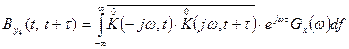 (14)
(14)
Величину 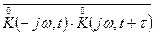 называют функцией корреляции системы с случайно изменяющимися параметрами.
называют функцией корреляции системы с случайно изменяющимися параметрами.
Введем обозначение:
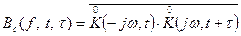 (15)
(15)
Тогда
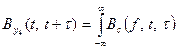 (16)
(16)
Параграф 2.7.3: Определение корреляционной функции отклика y3(t)
Корреляционную функцию отклика y3(t) можно определить формулой, аналогичной (16), если 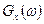 детерминированного воздействия в соответствии с определением энергетического спектра
детерминированного воздействия в соответствии с определением энергетического спектра 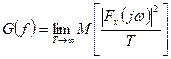 понимать характеристику
понимать характеристику
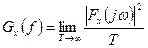 (17)
(17)
где 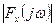 — спектр сигнала mx(t).
— спектр сигнала mx(t).
Параграф 2.7.4: Определение корреляционной функции отклика y2(t)
Корреляционную функцию отклика y2(t) детерминированной параметрической системы с характеристикой 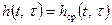 на стационарное случайное воздействие
на стационарное случайное воздействие 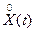 можно определить формулой, аналогичной (16), если заменить в ней
можно определить формулой, аналогичной (16), если заменить в ней 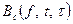 на
на 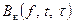 и под
и под 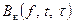 понимать
понимать 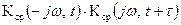 (18). Для детерминированной линейной параметрической безынерционной системы, у которой
(18). Для детерминированной линейной параметрической безынерционной системы, у которой 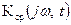 не зависит от частоты и равна Kср(t), формула (16) принимает вид:
не зависит от частоты и равна Kср(t), формула (16) принимает вид:
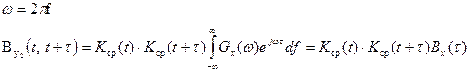 (19)
(19)
Если система линейна и стационарна, т.е. если ее параметры не изменяются во времени и 
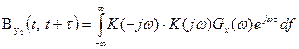 (20)
(20)
В соответствии со следствием теоремы Винера-Хинчина 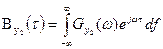 . Приравнивая правые части последнего равенства и уравнения (20), получим
. Приравнивая правые части последнего равенства и уравнения (20), получим
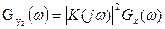 (21)
(21)
и
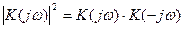 (22)
(22)
Формула (21) указывает закон преобразования энергетического спектра стационарного случайного процесса при его прохождении через стационарную линейную систему с КЧХ 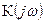 . ФЧХ линейной системы как и следовало ожидать не оказывает никакого влияния на закон преобразования энергетического спектра процесса. Вводя в рассмотрение временную функцию корреляции от неслучайной импульсной характеристики h(t)
. ФЧХ линейной системы как и следовало ожидать не оказывает никакого влияния на закон преобразования энергетического спектра процесса. Вводя в рассмотрение временную функцию корреляции от неслучайной импульсной характеристики h(t)
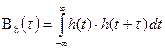 (23),
(23),
представляющую собой обратное преобразование Фурье от функции квадрат КЧХ на основании выражения (21) и теоремы о производной спектров (8 свойство преобразования Фурье).
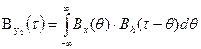 (24)
(24)
Т.о. задача о преобразовании энергетического спектра стационарного случайного процесса и его корреляционной функции при прохождении через стационарную линейную систему полностью решается формулами (20 — 24), если заданы частотная характеристика или импульсная реакция системы и энергетический спектр или корреляционная функция процесса на входе.
Параграф 2.7.5: Определение корреляционной функции отклика y1 (t)
Корреляционную функцию отклика y1(t) детерминированной линейной системы с характеристикой 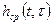 на детерминированное входное воздействие mx(t) можно определить с помощью (16), если учесть соотношения (17, 18):
на детерминированное входное воздействие mx(t) можно определить с помощью (16), если учесть соотношения (17, 18):
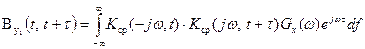 (25)
(25)
Если параметры системы не меняются во времени (если система стационарна), то
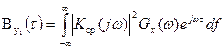 (26)
(26)
Энергетический спектр выхода: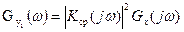 (27)
(27)
Учитывая, что 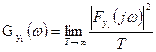 и (18) для спектров амплитуд входа
и (18) для спектров амплитуд входа 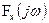 и выхода
и выхода 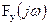 получаем из (27) известное ранее:
получаем из (27) известное ранее:
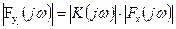
 2014-02-02
2014-02-02 1224
1224








