Принципы моделирования случайных элементов

Моделирование на ЭВМ случайного элемента подчиняется двум основным принципам:

1) сходство между случайным элементом-оригиналом 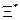и его моделью 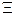состоит в совпадении (близости) вероятностных законов распределения или числовых характеристик;

2) всякий случайный элемент 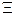определяется («конструируется») как некоторая борелевская функция от простейших случайных элементов, так называемых, базовых величин (БСВ).

Простейшим для моделирования на ЭВМ случайным экспериментом является эксперимент, заключающийся в бросании точки наудачу в промежуток [0, 1). Результатом этого эксперимента является координата точки. Математической моделью такого эксперимента является вероятностное пространство 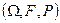, где 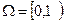- пространство элементарных событий (элементарное событие 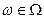заключается в том, что координата брошенной точки равна 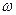); F - 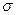-алгебра, порожденная интервалами из 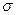; P - вероятностная мера, определенная для событий (подмножеств) 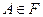и совпадающая с мерой Лебега, так что для события :

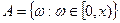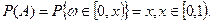(3.11)

Базовой случайной величиной (БСВ) на 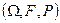будем называть непрерывную СВ

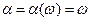(3.12)

Равномерно распределенную на полуинтервале [0, 1).

Функция распределенная БСВ имеет вид

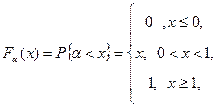(3.13)

а плотность распределения определяется формулой

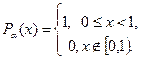
Будем обозначать закон распределения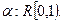

Математическое ожидание БСВ (первый начальный момент)

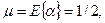
дисперсия (второй центральный момент)

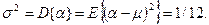
Наряду с простейшим экспериментом будем рассматривать составной случайный эксперимент, получающийся в результате r -кратного (r 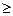1) повторения независимо друг от друга простейших экспериментов. Результатом составного случайного эксперимента является последовательность из r независимых БСВ 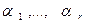таких, что

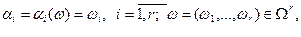
где 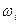- координата точки, брошенной наудачу в [0, 1) в i -м простейшем эксперименте.

Совместная плотность распределения вероятностей .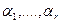

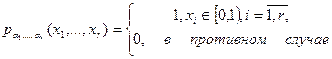
Согласно второму принципу моделирования случайных элементов, любой случайный элемент 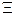представляется для некоторого натурального r в виде функции f(.) от r независимых БСВ

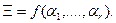
Таким образом, задача моделирования произвольного случайного элемента 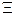* разбивается на две подзадачи:

1) моделирование на ЭВМ независимых БСВ ;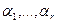

2) нахождение функции f(.) такой, чтобы случайный элемент 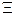обладал требуемыми вероятностным законом распределения и числовыми характеристиками.

Поэтому моделирующий алгоритм состоит из двух блоков (рис. 3.13)

Б1 — блок моделирования БСВ (общий для всех );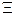

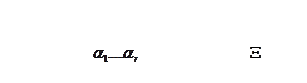
Рис.3.13 Моделирующий алгоритм БСВ

Б2 - блок функционального преобразования f(.) БСВ (различный для различных законов распределения вероятностей).

Для имитации одного и того же случайного элемента* может быть предложено несколько вариантов функциональных преобразований (способы построения f(.) будут описаны ниже). Обычно предпочтение отдается варианту f(.), требующему меньших вычислительных затрат; для этого используется понятие коэффициента использования БСВ.

Коэффициентом использования БСВ 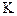назовем величину, обратную числу r базовых случайных величин, используемых для моделирования одной реализации случайного элемента *:

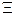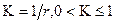
Величина 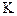является мерой вычислительных затрат на моделирование 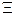*. Чем меньше 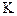, тем больше затраты. Целесообразно выбирать такую функцию f(.), для которой 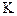принимает наибольшее значение.

Очевидно, чтобы моделировать на ЭВМ случайные элементы с заданным вероятностным законом распределения, необходимо уметь моделировать БСВ. БСВ 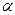является абсолютно непрерывной случайной величиной (СВ). Однако на ЭВМ приходится иметь дело с дискретными случайными величинами. Поэтому моделирование БСВ основано на аппроксимации непрерывной СВ 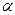дискретной случайной величиной (ДСВ) 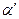. Опишем способ построения ДСВ .

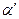Рассмотрим случай, когда представление целых неотрицательных чисел на ЭВМ осуществляется с помощью k двоичных разрядов (битов). Тогда С = {О, 1, 2 ^k - 1} — множество 2^k неотрицательных целых чисел, представимых в ЭВМ. Определим на (Q, 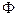, Р) дискретную случайную величину 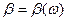следующим образом:

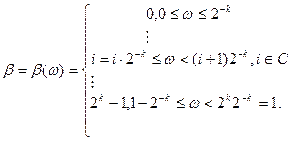(3.14)

Построение 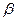проиллюстрируем с помощью рис.3.14. Разобьем промежуток [О, 1) на 2^k отрезков одинаковой длины 2^{- k}; для 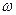, попадающих в промежуток 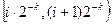полагаем 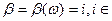С.

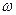
0 2^-k 2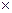2^-k…i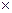2^-k (i+1) 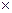2^-k…1-2^-k 1

Рис.3.14 Построение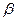

По построению распределение дискретной СВ 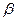является равномерным на множестве С, то есть все значения 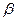равновероятны, действительно:

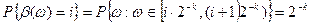(3.15)

Теперь перейдем от СВ 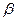к искомой ДСВ :

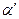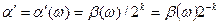(3.16)

Согласно (3.15)

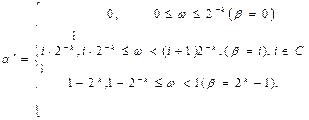
т.е. от целочисленной ДСВ 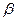мы перешли к ДСВ 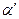со значениями в [О, 1).

Очевидно, все возможные значения 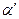определяются множеством С' = {0, 2^-k,…,1-2^-k} и являются равновероятными:

,

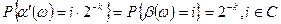т.е. закон распределения 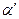является равномерным на .

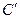Точность аппроксимации 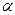с помощью 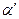устанавливается с помощью леммы.

Лемма. Для СВ 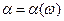и 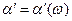, определенных на 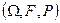и имеющих вид (3.12), (3.13) соответственно, равномерное уклонение удовлетворяет выражению.

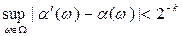(3.17)

Доказательство. Разобьем 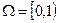на 2^k промежутков согласно рис.3.14. Пусть 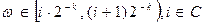. Тогда согласно (3.12) справедливо представление

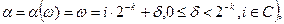
а согласно 3.16

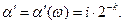
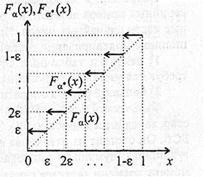Рис.3.15 Функция распределения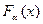

Поэтому

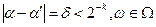
Отсюда заключаем справедливость (4.34).

Из (3.17) следует, что если 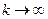, то последовательность 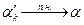равномерно по 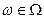. Таким образом, случайная величина 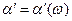является аппроксимацией для БСВ[1] 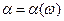; 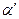называется в связи с этим квазиравномерной случайной величиной. Ее функция распределения 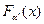изображена на рис.3.15 и аппроксимирует 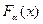с точностью 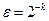. Между математическими ожиданиями величин 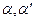справедливо соотношение

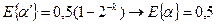
В табл.3.4 приведены соотношения между дисперсиями величин 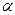и .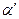

Таблица 3.4

k
	1,290	1,140	1,030	1,001	1,00

При достаточно больших значениях k (например, для ПЭВМ IBM PC AT 286

k =15, 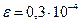; для ПЭВМ IBM PC AT 386, 486, 586 (Pentium) k = 31, 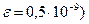величины отождествляют.