Количество движения материальной точки – это вектор, имеющий направление вектора скорости и равный произведению массы точки на ее скорость:
 . (6.1)
. (6.1)
 . (6.2)
. (6.2)
Производная по времени от количества движения материальной точки равна равнодействующей сил, действующих на точку.
Данное утверждение – это теорема об изменении количества движения материальной точки в дифференциальной форме. Выражение теоремы об изменении количества движения материальной точки в интегральной форме имеет вид
 . (6.3)
. (6.3)
Изменение  количества движения материальной точки за некоторый промежуток t–t0 времени равно импульсу
количества движения материальной точки за некоторый промежуток t–t0 времени равно импульсу 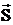 равнодействующей сил, действующих на точку за тот же промежуток времени
равнодействующей сил, действующих на точку за тот же промежуток времени
 (6.4)
(6.4)
Если сила  , то импульс силы
, то импульс силы
 . (6.5)
. (6.5)

Примеры решения задач
Задача 1
Трубка вращается с угловой скоростью  рад/с. Относительно трубки движется шарик М массой m = 0,2 кг со скоростью
рад/с. Относительно трубки движется шарик М массой m = 0,2 кг со скоростью  м/с. Определить модуль количества движения шарика в момент времени, когда расстояние ОМ = 0,4 м.
м/с. Определить модуль количества движения шарика в момент времени, когда расстояние ОМ = 0,4 м.
Решение
Количество движения определяется по формуле:
 ,
, 
где  – абсолютная скорость точки
– абсолютная скорость точки
 ,
, 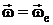 ,
, 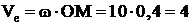 м/с.
м/с.
 м/с;
м/с; 

Ответ: 
 .
.
 Задача 2
Задача 2
Материальная точка М массой m = 1 кг равномерно движется по окружности со скоростью  м/с. Определить модуль импульса равнодействующей всех сил, действующих на эту точку за время ее движения из положения 1 в положение 2.
м/с. Определить модуль импульса равнодействующей всех сил, действующих на эту точку за время ее движения из положения 1 в положение 2.
Решение
Т.к. скорость точки в 1-ом и 2-ом положении постоянная, то модуль количества движения в 1-ом и 2-ом положении будут равны и определяются:

 ;
; 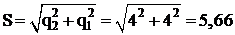
 .
.
Ответ: 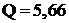
 .
.
 2017-11-30
2017-11-30 1539
1539
