2.1. Основные понятия и определения.
Прямолинейное движение точки, заданное уравнением
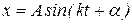 , (2.1)
, (2.1)
называется гармоническим колебательным движением.
Так как синус является периодической функцией, то координата 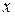 движущейся точки также изменяется периодически, принимая значения из интервала
движущейся точки также изменяется периодически, принимая значения из интервала 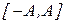 , т. е. точка
, т. е. точка 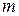 отклоняется последовательно в ту и другую сторону на величину
отклоняется последовательно в ту и другую сторону на величину 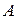 от начала координат
от начала координат 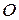 (рис.5).
(рис.5).
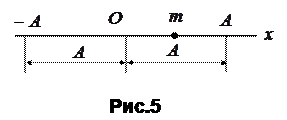 Постоянная
Постоянная 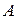 , равная величине наибольшего отклонения колеблющейся точки от ее среднего положения (точки
, равная величине наибольшего отклонения колеблющейся точки от ее среднего положения (точки  ), называется амплитудой колебаний точки.
), называется амплитудой колебаний точки.
Расстояние между двумя крайними положениями точки, равное удвоенной амплитуде, называется размахом колебаний.
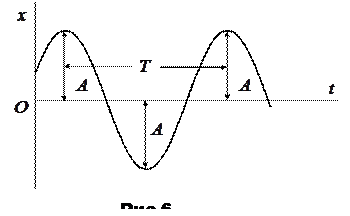 |
Из закона гармонических колебаний (2.1) видно, что графически они иллюстрируются синусоидой (рис.6).
Периодом колебаний 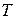 называется промежуток времени между двумя последовательными прохождениями точки через одно и то же положение с одной и той же скоростью.
называется промежуток времени между двумя последовательными прохождениями точки через одно и то же положение с одной и той же скоростью.
Аргумент синуса 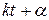 называется фазой колебаний точки, а величина
называется фазой колебаний точки, а величина 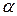 — начальной фазой.
— начальной фазой.
Так как период синуса равен 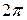 , то увеличение аргумента синуса на
, то увеличение аргумента синуса на 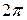 должно произойти за промежуток времени, равный периоду
должно произойти за промежуток времени, равный периоду 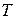 колебаний точки, т. е.
колебаний точки, т. е. 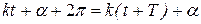 .
.
Отсюда находим
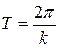 .
.
Число колебаний в 1 сек называется частотой. Ее величина
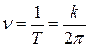 .
.
Следовательно 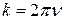 .
.
Из этой формулы виден физический смысл постоянной 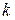 , называемой круговой или циклической частотой колебаний —число колебаний в
, называемой круговой или циклической частотой колебаний —число колебаний в 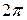 сек.
сек.
Частота 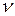 измеряется в герцах (Гц) (один герц—это одно колебание в секунду), а круговая частота
измеряется в герцах (Гц) (один герц—это одно колебание в секунду), а круговая частота 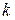 измеряется в рад/с.
измеряется в рад/с.
В дальнейшем величину 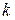 для краткости будем называть просто частотой.
для краткости будем называть просто частотой.
Выясним, под действием какой силы точка совершает прямолинейные гармонические колебания. Для этого решим прямую задачу динамики точки.
Дано: точка, масса которой 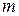 совершает прямолинейные гармонические колебания по закону
совершает прямолинейные гармонические колебания по закону
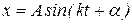 .
.
Определить: силу 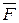 , вызвавшую это движение.
, вызвавшую это движение.
В соответствии с дифференциальным уравнением прямолинейного движения материальной точки (1.16) проекции искомой силы
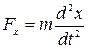 .
.
Вычислив соответствующие производные, получим:
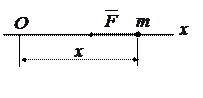
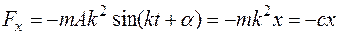 .
.
Таким образом, точка будет совершать гармонические колебания, если на эту точку, отклоненную от неподвижного центра 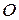 , действует сила
, действует сила 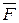 , направленная к центру
, направленная к центру 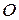 и пропорциональная расстоянию
и пропорциональная расстоянию
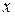 от этого центра. Проекция силы
от этого центра. Проекция силы 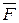 на ось
на ось 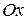
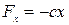 ,
,
где 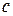 —постоянный коэффициент пропорциональности. Сила
—постоянный коэффициент пропорциональности. Сила 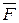 , как видно, стремится вернуть точку в равновесное положение
, как видно, стремится вернуть точку в равновесное положение 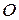 , где
, где 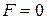 . Она называется восстанавливающей силой. Примером такой линейной восстанавливающей силы может служить сила упругости (сила реакции) пружины. В этом случае коэффициент пропорциональности
. Она называется восстанавливающей силой. Примером такой линейной восстанавливающей силы может служить сила упругости (сила реакции) пружины. В этом случае коэффициент пропорциональности 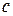 — коэффициент жесткости пружины, численно равный силе упругости ее при деформации, равной единице.
— коэффициент жесткости пружины, численно равный силе упругости ее при деформации, равной единице.
2. Свободные колебания в среде без сопротивления.
Пусть точка массы 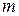 движется вдоль горизонтальной прямой под действием восстанавливающей силы
движется вдоль горизонтальной прямой под действием восстанавливающей силы 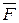 (рис.6). Прямолинейное движение материальной точки под действием только восстанавливающей силы называется свободным колебанием точки.
(рис.6). Прямолинейное движение материальной точки под действием только восстанавливающей силы называется свободным колебанием точки.
Для изучения свободного колебания составим дифференциальное уравнение движения точки, которое в данном случае имеет вид:
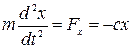 , или
, или 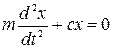 .
.
Разделив на массу точки 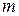 , и обозначив
, и обозначив 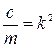 , запишем окончательно
, запишем окончательно
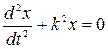 .
.
Полученное уравнение называется дифференциальным уравнением свободных колебаний материальной точки.
Для интегрирования этого однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами составим характеристическое уравнение
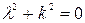 .
.
Его корни—числа мнимые
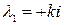 и
и 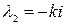 ,
,
следовательно, общее решение дифференциального уравнения (2.2) имеет вид
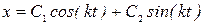 ,
,
где 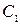 и
и 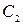 —постоянные интегрирования, определяемые начальными условиями. В качестве начальных условий зададим начальное положение точки и начальную скорость, т. е. при
—постоянные интегрирования, определяемые начальными условиями. В качестве начальных условий зададим начальное положение точки и начальную скорость, т. е. при 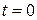 ,
, 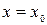 ,
, 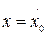 .
.
Чтобы определить значения постоянных интегрирования 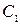 и
и 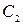 найдем уравнение, определяющее скорость точки, продифференцировав уравнение (2.3):
найдем уравнение, определяющее скорость точки, продифференцировав уравнение (2.3):
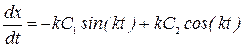 .
.
Подставив начальные условия в уравнения (2.3) и (2.4), найдем
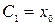 ,
, 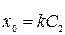 ,
,
откуда
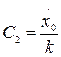 .
.
После подстановки найденных значений 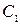 и
и 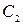 в (2.3) получаем уравнение движения рассматриваемой точки:
в (2.3) получаем уравнение движения рассматриваемой точки:
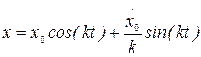 .
.
Уравнению (2.5) можно придать другой вид, введя вместо постоянных 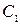 и
и 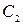 две другие постоянные
две другие постоянные 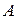 и
и 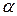 , положив
, положив
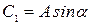 ;
; 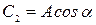 .
.
Выражение (2.3) примет следующий вид:
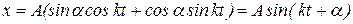 .
.
Произвольные постоянные 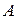 и
и 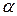 , как и
, как и 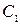 и
и 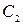 находятся по начальным условиям. Для их определения выразим
находятся по начальным условиям. Для их определения выразим 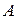 и
и 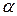 через
через
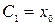 и
и 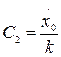 :
:
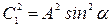 ,
, 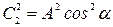 ,
,
Откуда
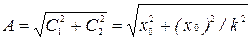 ,
, 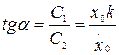 ,
, 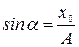 .
.
Значение амплитуды 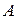 считаем положительным, угол
считаем положительным, угол 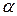 изменяется в пределах от
изменяется в пределах от 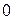 до
до 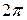 . Поэтому для его определения надо кроме величины тангенса знать еще знак синуса этого угла.
. Поэтому для его определения надо кроме величины тангенса знать еще знак синуса этого угла.
Окончательно, уравнение движения точки определяется следующим уравнением
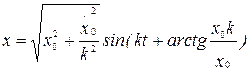 .
.
Уравнение —уравнение гармонических колебаний точки. Таким образом, установлено, что свободные колебания материальной точки под действием линейной восстанавливающей силы являются гармоническими колебаниями.
Так как 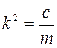 , то частота и период свободных колебаний определяются по формулам:
, то частота и период свободных колебаний определяются по формулам:
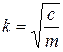 ,
,
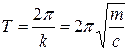 .
.
Как видно, частота и период свободных колебаний точки зависят только от массы этой точки 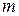 и от коэффициента
и от коэффициента 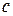 , характеризующего восстанавливающую силу, и не зависят от начальных условий движения.
, характеризующего восстанавливающую силу, и не зависят от начальных условий движения.
Период свободных колебаний 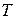 увеличивается при увеличении массы точки и уменьшается при увеличении коэффициента
увеличивается при увеличении массы точки и уменьшается при увеличении коэффициента 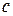 . Независимость периода колебаний от начальных условий называется изохронностью, а движение с таким периодом— изохронным.
. Независимость периода колебаний от начальных условий называется изохронностью, а движение с таким периодом— изохронным.
2.4. Вынужденные колебания при отсутствии сопротивления.
Рассмотрим колебания материальной точки, на которую кроме восстанавливающей силы 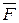 действует еще
действует еще 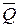 , проекция которой на ось
, проекция которой на ось 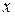 , направленную по траектории точки, изменяется по гармоническому закону
, направленную по траектории точки, изменяется по гармоническому закону
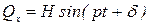 .
.
Эта сила называется возмущающей силой, а колебания, происходящие при действии такой силы, называются вынужденными.
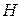 —амплитуда возмущающей силы;
—амплитуда возмущающей силы; 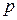 —частота возмущающей силы;
—частота возмущающей силы; 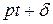 —фаза изменения возмущающей силы;
—фаза изменения возмущающей силы; 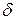 —начальная фаза изменения возмущающей силы.
—начальная фаза изменения возмущающей силы.
Пусть на прямолинейно движущуюся точку массы 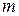 кроме восстанавливающей силы
кроме восстанавливающей силы 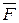 , пропорциональной отклонению точки от положения равновесия, действует только возмущающая сила
, пропорциональной отклонению точки от положения равновесия, действует только возмущающая сила 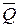 .Точка
.Точка 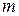 с приложенными к ней силами и оси координат изображены на рис.11. Основное уравнение динамики точки имеет вид:
с приложенными к ней силами и оси координат изображены на рис.11. Основное уравнение динамики точки имеет вид:
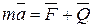 .
.
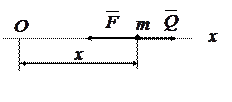
Спроектировав его на ось 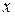 , получаем дифференциальное уравнение движения точки:
, получаем дифференциальное уравнение движения точки:
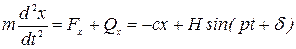 ,
,
где 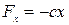 ,
, 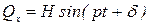 . Перенося все члены в левую часть и деля их на массу
. Перенося все члены в левую часть и деля их на массу 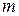 , получаем:
, получаем:
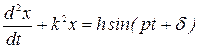 .
.
Здесь 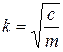 частота свободных колебаний;
частота свободных колебаний; 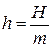 и имеет размерность ускорения.
и имеет размерность ускорения.
Уравнение — дифференциальное уравнение вынужденных колебаний точки при отсутствии сопротивления.
Решение этого уравнения зависит от соотношения между частотой 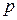 возмущающей силы и частотой
возмущающей силы и частотой 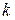 собственных колебаний. Тут возможны два случая: 1)
собственных колебаний. Тут возможны два случая: 1) 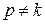 и 2)
и 2) 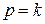 .
.
1. Случай отсутствия резонанса.
Найдем решение уравнения (2.23) для случая, когда частота возмущающей силы отлична от частоты свободных колебаний (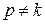 —нет резонанса.).
—нет резонанса.).
Уравнение (2.23)—неоднородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его решение складывается из общего решения однородного уравнения
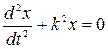
и частного решения данного уравнения (2.23):
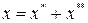
Однородное уравнение совпадает с дифференциальным уравнением собственных колебаний (2.2) и его решение может быть записано в двух эквивалентных формах (2.3) и (2.6):
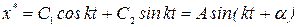 .
.
Частное решение неоднородного уравнения (2.23) определяется правой частью этого уравнения. В случае 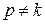 будем искать это решение в виде:
будем искать это решение в виде:
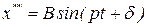 .
.
Постоянную 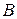 следует определить из условия, что функция
следует определить из условия, что функция 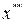 —частное решение уравнения (2.23) и, кроме того, подстановка
—частное решение уравнения (2.23) и, кроме того, подстановка 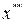 в это уравнение должна превратить его в тождество. Вычисляем необходимые производные по времени от
в это уравнение должна превратить его в тождество. Вычисляем необходимые производные по времени от 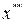 :
:
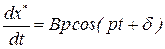 ,
, 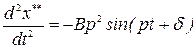 .
.
После подстановки в (2.23) получаем:
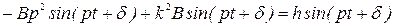 .
.
Полученное равенство будет выполняться при любом значении 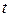 , если
, если
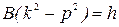 ,
,
откуда
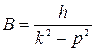 .
.
Подставляя найденное значение 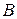 в (2.25), находим искомое частное решение неоднородного уравнения:
в (2.25), находим искомое частное решение неоднородного уравнения:
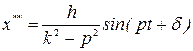 .
.
Общее решение уравнения (2.23) имеет окончательный вид
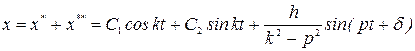 .
.
В амплитудной форме
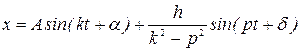 .
.
Решение (2.29) показывает, что колебания в рассматриваемом случае слагаются из: 1) колебаний с амплитудой 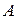 и частотой
и частотой 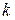 , называемых собственными колебаниями; 2) колебаний с амплитудой
, называемых собственными колебаниями; 2) колебаний с амплитудой 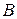 и частотой
и частотой 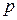 , которые называются вынужденными колебаниями.
, которые называются вынужденными колебаниями.
Постоянные интегрирования 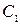 и
и 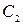 , или
, или 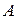 и
и 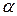 определяются по начальным условиям:
определяются по начальным условиям:
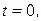
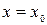 ,
, 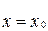 .
.
Предварительно найдем
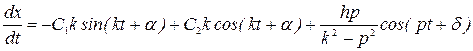 .
.
Подставляя эти значения в выражения для 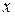 и
и 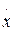 при
при 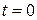 , получаем
, получаем
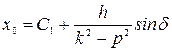 ,
, 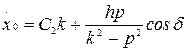 .
.
Отсюда
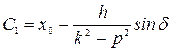 ,
, 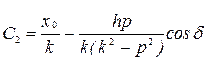 .
.
Амплитуда собственных колебаний 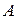 и начальная фаза
и начальная фаза 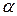 через
через 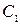 и
и 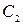 выражается формулами
выражается формулами
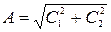 ,
, 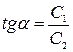
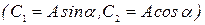 .
.
Следовательно, амплитуда и начальная фаза собственных колебаний при действии возмущающей силы зависят не только от начальных условий, но и от параметров этой силы, то есть собственные колебания в этом случае могут возникнуть не только из-за начальных условий, но и благодаря действию возмущающей силы даже при нулевых начальных условиях.
Рассмотрим вынужденные колебания, определяемые формулой
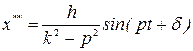
Частота 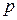 этих колебаний, как видно, равна частоте возмущающей силы, амплитуда
этих колебаний, как видно, равна частоте возмущающей силы, амплитуда
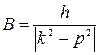 .
.
В зависимости от соотношения между частотами вынужденные колебания можно выразить в двух формах:
при 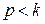
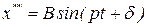 ,
,
при 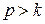
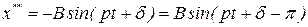 .
.
Следовательно, при 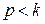 фаза вынужденных колебаний совпадает с фазой возмущающей силы. В этом случае сдвиг фаз между ними равен нулю, то есть вынужденные колебания и возмущающая сила достигают одновременно максимальных и минимальных значений.
фаза вынужденных колебаний совпадает с фазой возмущающей силы. В этом случае сдвиг фаз между ними равен нулю, то есть вынужденные колебания и возмущающая сила достигают одновременно максимальных и минимальных значений.
При 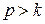 сдвиг фаз
сдвиг фаз 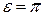 . Действительно, сдвиг фаз как разность фаз между возмущающей силой и вынужденными колебаниями
. Действительно, сдвиг фаз как разность фаз между возмущающей силой и вынужденными колебаниями
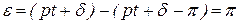 .
.
В этом случае вынужденные колебания находятся в противофазе по отношению к возмущающей силе, то есть, в частности, если возмущающая сила достигает максимума, то функция 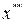 достигает минимума и наоборот.
достигает минимума и наоборот.
Итак, вынужденные колебания системы без сопротивления при 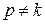 , возбуждаемые гармонической возмущающей силой:
, возбуждаемые гармонической возмущающей силой:
1) являются гармоническими колебаниями с постоянной амплитудой;
2) их частоты совпадают с частотой возмущающей силы;
3) они не зависят от начальных условий.
2. Случай резонанса.
Резонансом называется случай совпадения частот собственных колебаний и возмущающей силы, т. е.когда 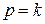 .
.
Как и в предыдущем случае, дифференциальное уравнение движения определяется уравнением
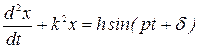
и оно имеет общее решение
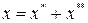 .
.
Здесь общее решение однородного уравнения
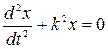 ,
,
по-прежнему имеет вид
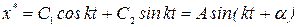 .
.
А вот частное решение 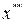 неоднородного уравнения будем искать в виде
неоднородного уравнения будем искать в виде
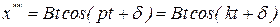 ,
,
-рассматривается случай 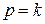 .
.
Постоянная 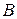 определяется из условия, что при подстановке
определяется из условия, что при подстановке 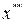 в рассматриваемое неоднородное дифференциальное уравнение это уравнение обращается в тождество.
в рассматриваемое неоднородное дифференциальное уравнение это уравнение обращается в тождество.
Вычисляем производные:
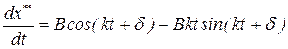 ;
;
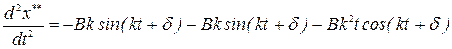
и подставляем значения 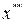 и
и 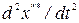 в уравнение:
в уравнение:
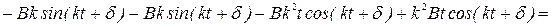
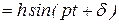 ,
,
или
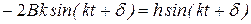 .
.
Приравнивая коэффициенты при синусе в левой и правой частях этого уравнения:
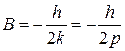 .
. 
Получаем, что частное решение
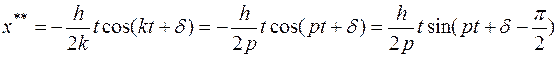 ,
,
а искомое общее решение уравнения
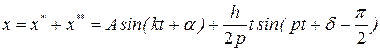 .
.
Уравнение показывает, что движение точки 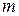 при резонансе является результатом наложения свободных и вынужденных колебаний точки, так же, как и при
при резонансе является результатом наложения свободных и вынужденных колебаний точки, так же, как и при 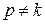 .
.
Рассмотрим вынужденные колебания при резонансе
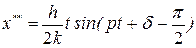 .
.
Основной особенностью этих колебаний является зависимость их амплитуды от времени
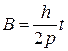 .
.
Амплитуда вынужденных колебаний при резонансе увеличивается пропорционально времени. Частота и период вынужденных колебаний при резонансе равны частоте 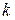 и периоду
и периоду 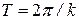 свободных колебаний точки. Фаза вынужденных колебаний отстает от фазы возмущающей силы величину
свободных колебаний точки. Фаза вынужденных колебаний отстает от фазы возмущающей силы величину 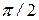 .
.
III. ВВЕДЕНИЕ В ДИНАМИКУ МЕХАНИЧЕСКОЙ СИСТЕМЫ.
3.1 Механическая система. Силы внешние и внутренние.
Механической системой называется такая совокупность материальных точек или тел, в которой положение или движение каждой точки или тела зависит от положения и движения всех остальных. Так, например, при изучении движения Земли и Луны относительно Солнца совокупность Земли и Луны является механической системой, состоящей из двух материальных точек, при разрыве снаряда на осколки мы рассматриваем осколки как механическую систему. Механической системой является любой механизм или машина.
Если расстояния между точками механической системы не изменяются при движении или покое системы, то такая механическая система называется неизменяемой.
Понятие неизменяемой механической системы позволяет изучать в динамике произвольное движение твердых тел. При этом, как в статике и кинематике, под твердым телом будем понимать такое материальное тело, у которого расстояния между каждыми двумя точками не изменяется при движении или покое тела. Любое твердое тело можно мысленно разбить на достаточно большое число достаточно малых частей, совокупность которых можно приближенно рассматривать как механическую систему. Так как твердое тело образует непрерывную протяженность, то для установления его точных (а не приближенных) свойств необходимо совершить предельный переход, предельное дробление тела, когда размеры рассматриваемых частей тела одновременно стремятся к нулю.
Таким образом, знание законов движения механических систем позволяет изучать законы произвольных движений твердых тел.
Все силы, действующие на точки механической системы, разделяют на внешние и внутренние силы.
Внешними силами по отношению к данной механической системе называются силы, действующие на точки этой системы со стороны материальных точек или тел, не входящих в систему. Обозначения: 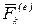 —внешняя сила, приложенная к
—внешняя сила, приложенная к 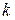 -ой точке;
-ой точке; 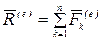 —главный вектор внешних сил;
—главный вектор внешних сил; 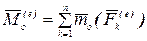 —главный момент внешних сил относительно полюса.
—главный момент внешних сил относительно полюса.
Внутренними силами называются силы, с которыми материальные точки или тела, входящие в данную механическую систему, действуют на точки или тела этой же системы. Другими словами, внутренние силы–это силы взаимодействия между точками или телами данной механической системы. Обозначения: 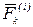 —внутренняя сила, приложенная к
—внутренняя сила, приложенная к 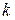 -ой точке;
-ой точке; 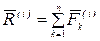 —главный вектор внутренних сил;
—главный вектор внутренних сил; 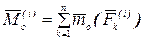 —главный момент внутренних сил относительно полюса.
—главный момент внутренних сил относительно полюса.
3.2 Свойства внутренних сил.
Первое свойство. Главный вектор всех внутренних сил механической системы равен нулю, то есть
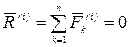 .
.
Второе свойство. Главный момент всех внутренних сил механической системы относительно любого полюса или оси равен нулю, то есть
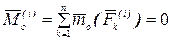 ,
, 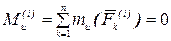 .
.
Для доказательства этих свойств заметим, что, так как внутренние силы—это силы взаимодействия материальных точек, входящих в систему, то по третьему закону Ньютона любые две точки системы (рис. 17) действуют друг на друга с силами 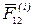 и
и 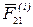 , равными по модулю и противоположными по направлению.
, равными по модулю и противоположными по направлению.
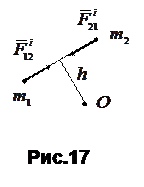 Таким образом, для каждой внутренней силы имеется прямопротивоположная внутренняя сила и, следовательно, внутренние силы образуют некоторое множество попарно противоположных сил. Но геометрическая сумма двух прямо противоположных сил равна нулю, поэтому
Таким образом, для каждой внутренней силы имеется прямопротивоположная внутренняя сила и, следовательно, внутренние силы образуют некоторое множество попарно противоположных сил. Но геометрическая сумма двух прямо противоположных сил равна нулю, поэтому
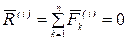 .
.
Как было показано в статике, геометрическая сумма моментов двух прямо противоположных сил относительно одного и того же полюса равна нулю, поэтому
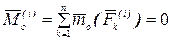 .
.
Аналогичный результат получается и при вычислении главного момента относительно оси
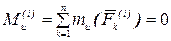 .
.
3.3 Дифференциальные уравнения движения механической системы.
Рассмотрим механическую систему, состоящую из 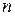 материальных точек, массы которых
материальных точек, массы которых 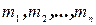 . Для каждой точки
. Для каждой точки 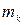 применим основное уравнение динамики точки
применим основное уравнение динамики точки
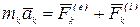 ,
, 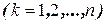 ,
,
или
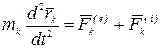 ,
,
где 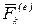 —равнодействующая внешних сил, приложенная к
—равнодействующая внешних сил, приложенная к 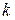 -ой точке, а
-ой точке, а 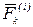 —равнодействующая внутренних сил.
—равнодействующая внутренних сил.
Систему 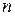 дифференциальных уравнений (3.3) называют дифференциальными уравнениями движения механической системы в векторной форме.
дифференциальных уравнений (3.3) называют дифференциальными уравнениями движения механической системы в векторной форме.
Проектируя векторные уравнения (3.3) на прямоугольные декартовые оси координат получим дифференциальные уравнения движения механической системы в координатной форме:
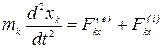 ,
,
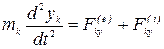 ,
,
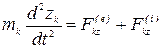 ,
,
Эти уравнение представляют собой систему 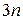 обыкновенных дифференциальных уравнений второго порядка. Следовательно, для нахождения движения механической системы по заданным силам и начальным условиям для каждой точки этой системы, необходимо проинтегрировать систему
обыкновенных дифференциальных уравнений второго порядка. Следовательно, для нахождения движения механической системы по заданным силам и начальным условиям для каждой точки этой системы, необходимо проинтегрировать систему 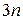 дифференциальных уравнений. Интегрирование системы дифференциальных уравнений (3.4), вообще говоря, сопряжено со значительными, зачастую непреодолимыми математическими трудностями. Однако в теоретической механике разработаны методы, которые позволяют обойти основные трудности, возникающие при использовании дифференциальных уравнений движения механической системы в форме (3.3) или (3.4). К их числу относятся методы, которые дают общие теоремы динамики механической системы, устанавливающие законы изменения некоторых суммарных (интегральных) характеристик системы в целом, а не закономерности движения отдельных её элементов. Это так называемые меры движения—главный вектор количества движения; главный момент количества движения; кинетическая энергия. Зная характер изменения этих величин, удается составить частичное, а иногда и полное представление о движении механической системы.
дифференциальных уравнений. Интегрирование системы дифференциальных уравнений (3.4), вообще говоря, сопряжено со значительными, зачастую непреодолимыми математическими трудностями. Однако в теоретической механике разработаны методы, которые позволяют обойти основные трудности, возникающие при использовании дифференциальных уравнений движения механической системы в форме (3.3) или (3.4). К их числу относятся методы, которые дают общие теоремы динамики механической системы, устанавливающие законы изменения некоторых суммарных (интегральных) характеристик системы в целом, а не закономерности движения отдельных её элементов. Это так называемые меры движения—главный вектор количества движения; главный момент количества движения; кинетическая энергия. Зная характер изменения этих величин, удается составить частичное, а иногда и полное представление о движении механической системы.
IV. ОСНОВНЫЕ (ОБЩИЕ) ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ И СИСТЕМЫ
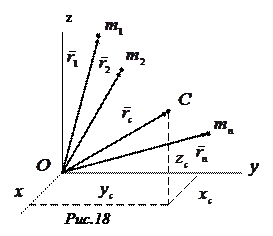 4.1 Теорема о движении центра масс.
4.1 Теорема о движении центра масс.
4.1.1.Центр масс механической системы.
Рассмотрим механическую систему, состоящую из 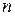 материальных точек, массы которых
материальных точек, массы которых 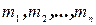 .
.
Массой механической системы, состоящей из 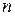 материальных точек, будем называть сумму масс точек системы:
материальных точек, будем называть сумму масс точек системы:
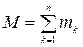 .
.
Определение. Центром масс механической системы называется геометрическая точка 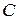 , радиус вектор которой определяется по формуле:
, радиус вектор которой определяется по формуле:
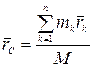 ,
,
где 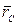 —радиус-вектор центра масс;
—радиус-вектор центра масс; 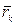 —радиус-векторы точек системы;
—радиус-векторы точек системы; 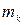 —их массы (рис.18).
—их массы (рис.18).
Проецируя (4.1) на декартовые оси координат получим формулы для координат центра масс
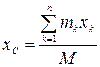 ;
; 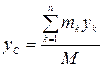 ;
; 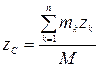 .
.
Центр масс является не материальной точкой, а геометрической. Он может не совпадать ни с одной материальной точкой механической системы. В однородном поле силы тяжести центр масс совпадает с центром тяжести. Это, однако, не означает, что понятия центра масс и центра тяжести одинаковы. Понятие центра масс применимо к любым механическим системам, а понятие центра тяжести применимо только к механическим системам, находящимся под действием сил тяжести (то есть притяжения к Земле). Так, например, в небесной механике при рассмотрении задачи о движении двух тел, например Земли и Луны, можно рассматривать центр масс этой системы, но нельзя рассматривать центр тяжести.
Таким образом, понятие центра масс более широкое, чем понятие центра тяжести.
4.1.2. Теорема о движении центра масс механической системы.
Теорема. Центр масс механической системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему, то есть
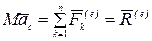 .
.
Здесь 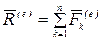 —главный вектор внешних сил.
—главный вектор внешних сил.
Проектируя обе части этого векторного равенства на координатные оси, получим:
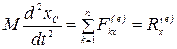 ,
,
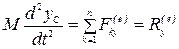 ,
,
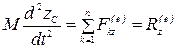 ,
,
где 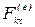 ,
, 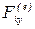 ,
, 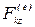 —проекции силы
—проекции силы 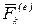 ;
;
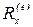 ,
, 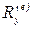 ,
, 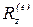 —проекции главного вектора внешних сил
—проекции главного вектора внешних сил 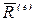 на оси координат.
на оси координат.
Уравнения — дифференциальные уравнения движения центра масс механической системы в проекциях на декартовые оси координат.
Из уравнений следует, что только одними внутренними силами нельзя изменить характер движения центра масс механической системы. Внутренние силы могут оказывать косвенное влияние на движение центра масс только через внешние силы. Например, в автомобиле внутренние силы, развиваемые двигателем, влияют на движение центра масс через силы трения колес с дорогой.
4.1.3. Законы сохранения движения центра масс
(следствия из теоремы).
Из теоремы о движении центра масс можно получить следующие следствия.
Следствие 1. Если главный вектор внешних сил, действующих на систему, равен нулю, то её центр масс находится в покое или движется прямолинейно и равномерно.
Действительно, если главный вектор внешних сил 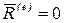 , то из уравнения (4.2):
, то из уравнения (4.2):
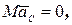
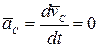 ,
, 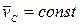 .
.
Если, в частности, начальная скорость центра масс 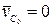 , то центр масс находится в покое. Если же начальная скорость
, то центр масс находится в покое. Если же начальная скорость 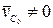 , то центр масс движется прямолинейно и равномерно.
, то центр масс движется прямолинейно и равномерно.
Следствие 2. Если проекция главного вектора внешних сил на какую-либо неподвижную ось равна нулю, то проекция скорости центра масс механической системы на эту ось не изменяется.
Это следствие вытекает из уравнений (4.3). Пусть, например, 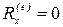 , тогда
, тогда
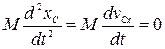 ,
,
отсюда 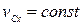 . Если при этом в начальный момент
. Если при этом в начальный момент 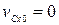 , то:
, то:
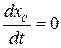 ,
, 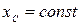 ,
,
то есть проекция центра масс механической системы на ось 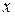 в этом случае не будет перемещаться вдоль оси
в этом случае не будет перемещаться вдоль оси 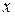 . Если же
. Если же 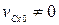 , то проекция центра масс на ось
, то проекция центра масс на ось 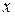 движется равномерно.
движется равномерно.
4.2 Количество движения точки и системы.
Теорема об изменении количества движения.
4.2.1. Количество движения точки и системы.
Определение. Количеством движения материальной точки 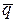 называется вектор, равный произведению массы точки
называется вектор, равный произведению массы точки 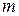 на её скорость
на её скорость 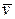 , то есть
, то есть
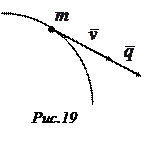
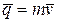 .
.
Вектор 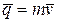 коллинеарен вектору
коллинеарен вектору 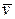 и направлен по касательной к траектории материальной точки (рис.19).
и направлен по касательной к траектории материальной точки (рис.19).
Количество движения точки в физике часто называют импульсом материальной точки.
Размерность количества движения в СИ—кг·м/c или Н·с.
Определение. Количеством движения механической системы называется вектор 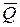 , равный векторной сумме количеств движений (главный вектор количеств движений) отдельных точек, входящих в систему, то есть
, равный векторной сумме количеств движений (главный вектор количеств движений) отдельных точек, входящих в систему, то есть
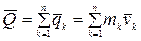
Проекции количества движения на прямоугольные декартовые оси координат:
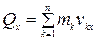 ;
; 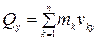 ;
; 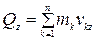
Вектор количества движения системы 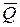 в отличие от вектора количества движения точки
в отличие от вектора количества движения точки 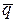 не имеет точки приложения. Вектор количества движения точки приложен в самой движущейся точке, а вектор
не имеет точки приложения. Вектор количества движения точки приложен в самой движущейся точке, а вектор 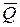 является свободным вектором.
является свободным вектором.
Лемма количеств движения. Количество движения механической системы равно массе всей системы, умноженной на скорость её центра масс, то есть
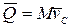
Доказательство. Из формулы (4.1), определяющей радиус-вектор центра масс, следует:
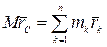 .
.
Возьмем от обеих частей производную по времени
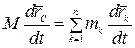 , или
, или 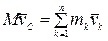 .
.
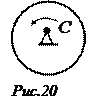 Отсюда получим
Отсюда получим 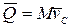 , что и требовалось доказать.
, что и требовалось доказать.
Из формулы (4.8) видно, что если тело движется так, что его центр масс остается неподвижным, то количество движения тела равно нулю. Например, количество движения тела, вращающегося вокруг неподвижной оси, проходящей через его центр масс (рис.20),
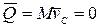 , т.к.
, т.к. 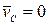
4.2.2. Теорема об изменении количества движения механической системы
в дифференциальной форме.
Теорема. Производная по времени от количества движения механической системы равна геометрической сумме (главному вектору) внешних сил, действующих на эту систему, т.е.
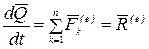 .
.
Доказательство. Рассмотрим механическую систему, состоящую из 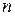 материальных точек, массы которых
материальных точек, массы которых 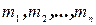 ;
; 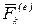
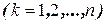 —равнодействующая внешних сил, приложенная к
—равнодействующая внешних сил, приложенная к 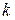 -ой точке. В соответствии с леммой количества движения—формула (4.8):
-ой точке. В соответствии с леммой количества движения—формула (4.8):
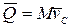 .
.
Возьмем от обеих частей этого равенства производную по времени
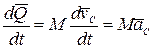 .
.
Правая часть этого равенства из теоремы о движении центра масс—формула (4.2):
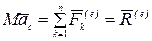 .
.
Окончательно:
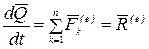
и теорема доказана.
В проекциях на прямоугольные декартовые оси координат:
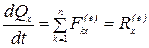 ;
; 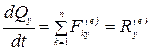 ;
; 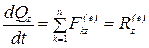 ,
,
то есть производная по времени от проекции количества движения механической системы на какую либо координатную ось равна сумме проекций (проекции главного вектора) всех внешних сил системы на ту же ось.
4.2.3. Законы сохранения количества движения
(следствия из теоремы)
Следствие 1. Если главный вектор всех внешних сил механической системы равен нулю, то количество движения системы постоянно по величине и направлению.
Действительно, если 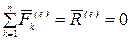 , то из теоремы об изменении количества движения, т. е. из равенства (4.9) следует, что
, то из теоремы об изменении количества движения, т. е. из равенства (4.9) следует, что
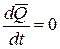 .
.
Отсюда 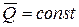 .
.
Следствие 2. Если проекция главного вектора всех внешних сил механической системы на некоторую неподвижную ось равна нулю, то проекция количества движения системы на эту ось остается постоянной.
Пусть проекция главного вектора всех внешних сил на ось 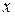 равна нулю:
равна нулю: 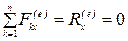 . Тогда из первого равенства (4.10):
. Тогда из первого равенства (4.10):
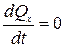 .
.
Отсюда 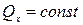 .
.
4.2.4. Теорема об изменении количества движения механической системы в интегральной форме.
Элементарным импульсом силы называется векторная величина 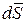 , равная произведению вектора силы
, равная произведению вектора силы 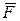 на элементарный промежуток времени
на элементарный промежуток времени 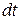
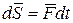 .
.
Направление элементарного импульса совпадает с направлением вектора силы.
Импульс силы за конечный промежуток времени 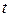 равен определенному интегралу от элементарного импульса
равен определенному интегралу от элементарного импульса
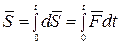 .
.
Если сила 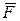 постоянна по величине и направлению (
постоянна по величине и направлению (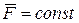 ), то ее импульс за время
), то ее импульс за время 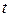 равен:
равен:
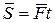 .
.
Проекции импульса силы на оси координат:
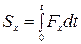 ,
, 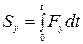 ,
, 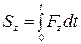 .
.
Докажем теорему об изменении количества движения механической системы в интегральной форме.
Теорема. Изменение количества движения механической системы за некоторый промежуток времени равно геометрической сумме импульсов внешних сил системы за этот же промежуток времени, т.е.
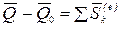
Доказательство. Пусть в момент времени 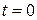 количество движения механической системы равно
количество движения механической системы равно 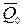 , а в момент времени
, а в момент времени 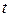 —
— 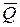 ;
; 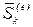 —импульс внешней силы, действующей на
—импульс внешней силы, действующей на 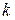 -ю точку за время
-ю точку за время 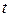 .
.
Используем теорему об изменении количества движения в дифференциальной форме—равенство (4.9):
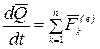 .
.
Умножая обе части этого равенства на 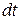 и интегрируя в пределах от
и интегрируя в пределах от 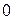 до
до 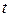 , получим
, получим
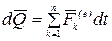 ,
, 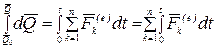 ,
, 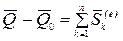 .
.
Теорема об изменении количества движения в интегральной форме доказана.
В проекциях на оси координат согласно (4.14):
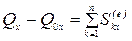 ,
,
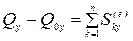 ,
,
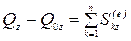 .
.
4.3. Теорема об изменении кинетического момента.
4.3.1. Кинетический момент точки и системы.
В статике были введены и широко использовались понятия моментов силы относительно полюса и оси. Так как количество движения материальной точки 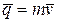 является вектором, то можно определить его моменты относительно полюса и оси таким же образом, как определяются моменты силы.
является вектором, то можно определить его моменты относительно полюса и оси таким же образом, как определяются моменты силы.
Определение. Кинетическим моментом материальной точки 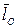 относительно полюса
относительно полюса 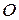 называется момент её вектора количества движения относительно того же полюса
называется момент её вектора количества движения относительно того же полюса 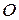 , т. е.
, т. е.
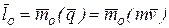 .
.
Кинетический момент материальной точки относительно полюса 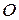 представляет собой вектор
представляет собой вектор 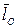 (рис.22), направленный перпендикулярно плоскости, содержащей вектор
(рис.22), направленный перпендикулярно плоскости, содержащей вектор 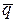 и полюс
и полюс 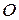 в ту
в ту
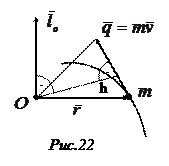 сторону, откуда вектор
сторону, откуда вектор 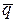 относительно полюса
относительно полюса 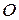 виден направленным против вращения часовой стрелки. Модуль вектора
виден направленным против вращения часовой стрелки. Модуль вектора 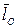 равен произведению модуля
равен произведению модуля 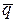 на плечо
на плечо 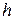 —длина перпендикуляра, опущенного из полюса
—длина перпендикуляра, опущенного из полюса 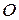 на линию действия вектора
на линию действия вектора 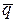 :
:
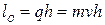
Кинетический момент относительно полюса может быть представлен в виде векторного произведения: кинетический момент материальной точки относительно полюса равен векторному произведению радиус вектора 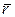 , проведенного из полюса
, проведенного из полюса 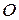 в точку
в точку 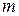 на вектор количества движения
на вектор количества движения 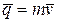 :
:
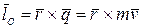
 Определение. Кинетическим моментом материальной точки
Определение. Кинетическим моментом материальной точки 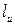 относительно оси
относительно оси 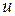 называется момент её вектора количества движения относительно той же оси
называется момент её вектора количества движения относительно той же оси 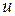 , т. е.
, т. е.
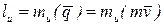 .
.
Кинетический момент 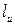 материальной точки
материальной точки 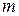 относительно оси
относительно оси 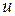 (рис.23) равен взятому со знаком плюс или минус произведению проекции вектора
(рис.23) равен взятому со знаком плюс или минус произведению проекции вектора 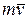 на плоскость перпендикулярную к оси
на плоскость перпендикулярную к оси 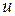 , на плечо этой проекции
, на плечо этой проекции 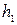 :
:
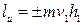 ,
,
где плечо 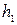 —длина перпендикуляра опущенного из точки
—длина перпендикуляра опущенного из точки 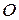 пересечения оси
пересечения оси 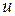 с плоскостью на линию действия проекции
с плоскостью на линию действия проекции 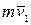 , при этом
, при этом 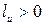 , если, смотря навстречу оси
, если, смотря навстречу оси 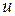 , видно проекцию
, видно проекцию 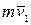 относительно точки
относительно точки 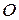 направленной против вращения часовой стрелки, и
направленной против вращения часовой стрелки, и 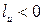 в противном случае.
в противном случае.
Размерность кинетического момента в СИ—кг·м2/с, или Н·м·с.
Определение. Кинетическим моментом или главным моментом количества движения 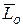 механической системы относительно полюса называется вектор, равный геометрической сумме кинетических моментов всех материальных точек системы относительно этого полюса:
механической системы относительно полюса называется вектор, равный геометрической сумме кинетических моментов всех материальных точек системы относительно этого полюса:
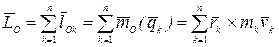 .
.
Определение. Кинетическим моментом или главным моментом количества движения механической системы 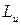 относительно оси называется алгебраическая сумма кинетических моментов всех материальных точек систем
относительно оси называется алгебраическая сумма кинетических моментов всех материальных точек систем
 2015-04-23
2015-04-23 5091
5091