Применение понятия производной и интеграла

Мы не будем приводить здесь подробное определение производной и интеграла. Для решения задач нам понадобятся лишь небольшой набор формул.

Производная:

 

 

 

 

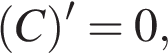
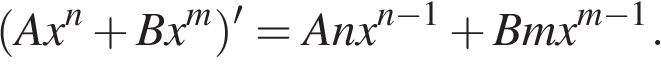
где A, B и 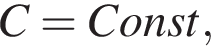то есть постоянные величины.

Интеграл:

 

 

 

 

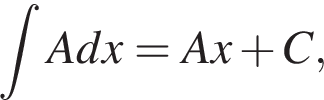
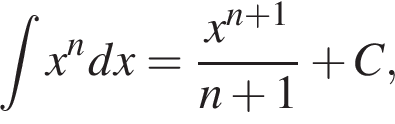
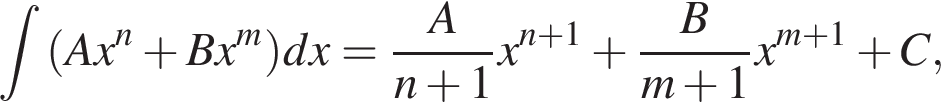
Теперь посмотрим, как понятие производной и интеграла применимо к физическим величинам. В математике производная обозначается «'», в физике производная по времени обозначается «∙» над функцией.

Скорость:

 

 

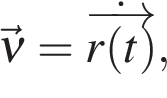
то есть скорость является производной от радиус-вектора.

Для проекции скорости:

 

 

 

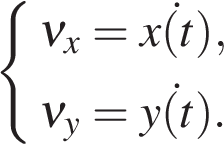
Ускорение:

 

 

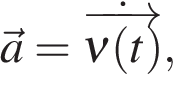
то есть ускорение является производной от скорости.

Для проекции ускорения:

 

 

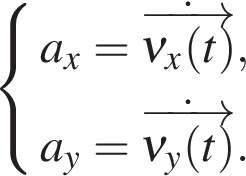
Таким образом, если известен закон движения 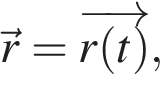то легко можем найти и скорость и ускорение тела.

Теперь воспользуемся понятием интеграла.

Скорость:

 

 

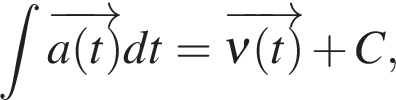
то есть, скорость можно найти как интеграл по времени от ускорения.

 

 

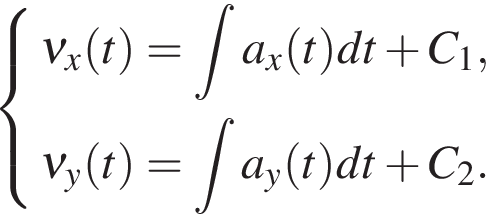
Радиус-вектор:

 

 

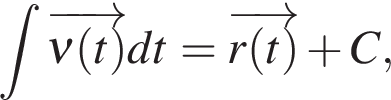
то есть, радиус-вектор можно найти, взяв интеграл от функции скорости.

 

 

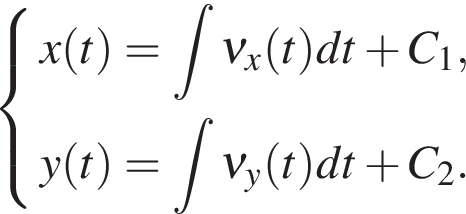
Таким образом, если известна функция 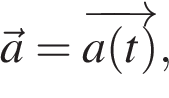то легко можем найти и скорость, и закон движения тела.

Константы в формулах определяются из начальных условий — значения 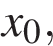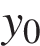и в момент времени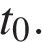

 

Треугольник скоростей и треугольник перемещений