2017-11-30
1897
5.1. Первое начало термодинамики:
,
где Q - количество теплоты, сообщенное газу в рассматриваемом процессе;
A - работа, совершенная газом; ΔU – изменение внутренней энергии газа в данном процессе.
5.2. Работа, совершаемая газом:
.
5.3. Для любого процесса, происходящего с идеальным газом, изменение внутренней энергии рассчитывается по одной и той же формуле:
.
5.4. Количество теплоты и работа, совершаемая газом, зависит от вида процесса.
· Изотермический процесс: T = const; ΔT = 0; ΔU = 0;
.
· Изохорический процесс: V= const; ΔV = 0; A = 0;
.
· Изобарический процесс: Р = const;
, 
.
· Адиабатный процесс – процесс, при котором отсутствует теплообмен между системой и окружающей средой:
Q адиаб = 0,
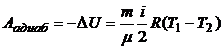
или
где γ – показатель адиабаты, 
5.5. В адиабатном процессе изменяются все параметры идеального газа: Р, V и Т. Уравнения адиабатного процесса имеют вид уравнений Пуассона:
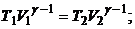
Пример 4. Азот, занимавший при давлении Р1 = 105Паобъем V 1 = 10 л, расширяется вдвое. Найти конечное давление и работу, совершенную газом при следующих процессах: а) изобарном; в) изотермическом; c) адиабатном (рис.1).
Дано: Р 1 = 105 Па; V 1=10 л = 10∙10-3 м3; V 2/ V 1 = 2; i = 5.
Найти: Р 2 ; А 1-2; Р 3; А 1-3 ; Р 4; А 1-4. Рис.1
Решение. 1.Рассмотрим изобарический процесс 1-2: Р = const, следовательно, Р 2 = Р 1 ;
Дж.
2. При изотермическом расширении 1-3 давление уменьшается.
По закону Бойля-Мариотта:
;
, 
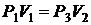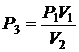Па;
, 
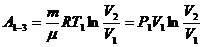Дж.
3. В адиабатном процессе 1-4 Р 4 найдем из уравнения Пуассона: 
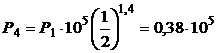Па.
Работа, совершаемая газом при адиабатном расширении, равна убыли внутренней энергии газа:
По уравнению Менделеева - Клапейрона:
и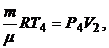 
следовательно,
Дж.
Ответ: Р 2 = 105; А 1-2 = 1000 Дж; Р 3 = 0,5∙105 Па; А 1-3 = 690Дж;
Р 4 = 0,38∙105 Па; А 1-4 = 600 Дж.
Пример 5. 1моль идеального газа, имеющий первоначально температуру T 1 = 290 К,расширяется изобарически до тех пор, пока его объем не возрастает в 2 раза. Затем газ охлаждается изохорически до первоначальной температуры T 1 . Определить приращение внутренней энергии газа Δ U, работу А, совершаемую газом, количество полученной газом теплоты Q.
Рис.2
Дано: 
моль; Р 2 = Р 1; V 2 = 2V 1; V 3 = V 2; Т 3 = Т 1.
Найти: Δ U 1-2-3; А 1-2-3; Q 1-2-3.
Решение. Изобразим графики процессов в координатах Р-V (рис.2). Внутренняя энергия газа – это функция состояния; ее изменение не зависит от пути перехода системы из начального состояния в конечное.
Поэтому
,
но так как Т 3 = Т 1 (по условию задачи), то Δ U 1-2-3 = 0.
Работа, совершаемая газом:
Так как в изохорическом процессе не происходит изменения объема (Δ V =0), то А 2-3 = 0, следовательно,
Количество теплоты, полученное в сложном процессе 1-2-3, найдем из первого начала термодинамики:
Учитывая, что Δ U 1-2-3 = 0, имеем
Произведем вычисления:
Дж.
Ответ: ∆ U =0, Q1-2-3 = A1-2-3 = 2,41∙103Дж.
Пример 6. Углекислый газ (СО2), начальная температура которого 360 К, адиабатически сжимается до 1/20 своего первоначального объема. Определить: а) температуру газа в конце сжатия Т 2; б) изменение внутренней энергии Δ U; в) работу, совершенную над газом при сжатии, А. (Масса газа 20 г.)
Дано: m =20 г=20ּ10-3 кг; μ =44 г/моль=44 10-3 кг/моль; Т 1 = 360 К; i = 6;
V 2 = 1/20 V 1.
Найти: T 2; Δ U; А.
Решение. 1. Температуру в конце сжатия определим по уравнению адиабатного процесса, записанного для переменных Т и V:
или 
. (1)
Так как СО2 – трехатомный газ, i = 6 и γ = 4/3.
2. Адиабатный процесс происходит без теплообмена и изменение внутренней энергии происходит за счет работы внешних сил, т. е. Q = 0;
Δ U = – A.
Тогда работа Аад газа в адиабатном процессе:
.
Изменение внутренней энергии определяется по формуле:
. (2)
Произведя подстановку (см. формулу (1)), получим:
.
Проверим размерность:
Дж.
Произведем вычисления:
К;
кДж.
Ответ: Т 2 = 985К; ΔU = 7,05 кДж; А = - 7,05 кДж.
