Взаимосвязь определителя большего порядка и меньшего порядка. Разложение по строке

Запишем разложение определителя порядка 3.

= .

Вынесем за скобку элементы первой строки (они есть в 2 из 6 слагаемых): .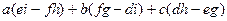

То, что получилось в скобках, называют алгебраическими дополнениями элементов соответственно .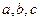

Выражение в 1-й скобке 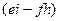называется алгебраическим дополнением к элементу 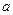, соответственно

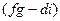- алгебраическим дополнением к 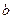, 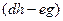- алгебраическим дополнением к .

 

Заметим, что , , .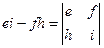

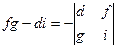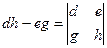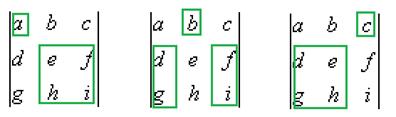
Если для элемента 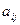и вычеркнуть всю строку и весь столбец, где он находится, образуется подматрица порядка (n-1). Определитель подматрицы порядка (n-1), которая получилась путём вычёркивания строки номер i и столбца номер j, называется дополняющим минором к элементу 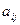. Всего таких миноров 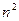, например для матрицы 3 порядка их будет 9 штук. Минор, соответствующий элементу 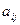, обозначается .

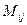Мы видим, что в одних случаях алгебраическое дополнение равно минору, а где-то противоположно ему по знаку. Взаимосвязь алгебраических дополнений и миноров для произвольных i,j:

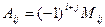, то есть знаки меняются в шахматном порядке, для верхнего левого элемента 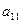знак «+».

Итак, определители можно вычислять разложением по строке:

= .

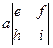
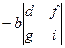
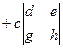Общая запись в произвольных обозначениях: .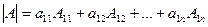

Разложение возможно по любой строке или по любому столбцу. Так, например, в той же рассмотренной ранее записи можно собрать пары слагаемых, содержащих 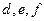и точно так же вынести за скобку, получится = =

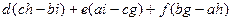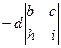
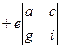
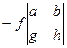= здесь чередование знака начинается с минуса, что и должно быть в соответствии с шахматным порядком, о чём сказано выше.

 

Лемма. Если матрица треугольная, то .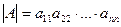

Доказательство.

Пусть дан определитель .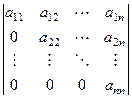

Если разложить его по первому столбцу, где всего один ненулевой элемент и остальные нулей, то сразу переходим к минору меньшего порядка:

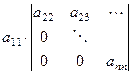+ 0 +... + 0.

для него получается аналогичное действие, тогда на следующем шаге получаем 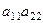умножаются на определитель треугольной матрицы, у которой угловой элемент 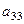. Продолжая этот процесс, получим .

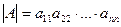Замечание. Для диагональных матриц верен такой же факт, ведь диагональная это частный случай треугольной.

 

Пример.

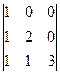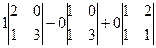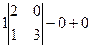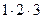= = = = 6.

Приведение к треугольному виду очень часто используется для вычисления определителей. Метод Гаусса, который будет подробно изучен в теме «системы уравнений», в полной мере может применяться и для вычисления определителей. Если обнулить элементы ниже главной диагонали, то вычисление определителя сильно упростится.

 

 

§ 3. Обратная матрица.

Определение. Матрица называется вырожденной, если 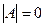, и невырожденной, если .

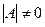Определение. Пусть 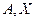- квадратные матрицы. Если 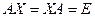то 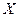называется обратной матрицей для матрицы .

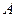Обозначение: Обратная матрица обозначается .

 

Замечание. Для чисел, которые являются матрицами порядка 1, обратный элемент вычисляется известным образом, например , .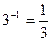

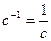Итак, 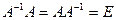. Но оказывается, что не для любой квадратной матрицы существует обратная.

Лемма. Обратная матрица существует тогда и только тогда, когда А невырожденная.

Доказательство. Для доказательства рассмотрим 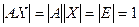. Если 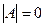то 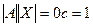, то есть существовало бы такое число, которое при умножении на 0 даёт результат 1, но это невозможно. Получили противоречие.

Формула вычисления элементов обратной матрицы: .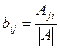

Алгоритм нахождения ,.

1. Проверить невырожденность с помощью определителя.

2. Составить матрицу из дополняющих миноров M_ij.

3. Изменить знаки в шахматном порядке, то есть домножить на (-1)^i+j, где i,j - номера строки и столбца.

Получатся алгебраические дополнения A_ij.

4. Транспонировать полученную матрицу.

5. Поделить на определитель исходной матрицы.

Пример. Найти .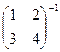

Решение. 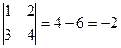. Вывод: 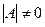, существует обратная матрица.

Матрица из миноров: .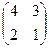

Матрица из алг. дополнений: .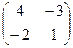

Транспонируем её: .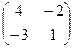

Делим её на определитель, и записываем ответ: = .

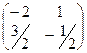Можно сделать проверку: = .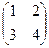

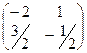Пример. Найти обратную матрицу: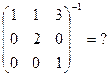

Решение. 1) 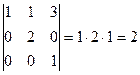. 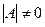, существует .

2) Запишем матрицу, состоящую из всех возможных миноров , которых существует 9 штук: = .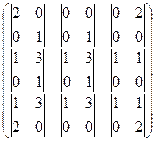

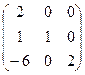3) Матрица из алгебраических дополнений: .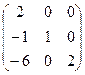

(т.е. в шахматном порядке изменили знаки, там где сумма номеров строки и столбца нечётна).

Транспонируем её: 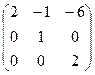. Делим на определитель, равный 2, итог: = .

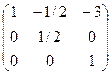Докажем, что не существует различных «обратной слева» и «справа» матриц. Так как коммутативность в общем случае не выполняется, то вовсе не очевидно, что обратная матрица единственна, ведь можно предположить, что левая обратная и правая обратная - различны.

Лемма. Если 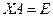и , то .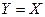

Доказательство. Пусть 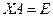и . По закону ассоциативности, можно записать такое равенство: .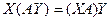

Но тогда получается 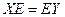, то есть .

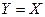ЛЕКЦИЯ № 3. 19.09.2017

 

§ 4. Ранг матрицы.

Для прямоугольных матриц не существует понятие определителя, однако там можно выбирать квадратные подматрицы, и для них определитель вычислить можно. Если задать какие-нибудь k номеров строк и k номеров столбцов, то на пересечениях, очевидно, получится минор из k² элементов. Он может быть вырожденным либо нет. Существует минор максимального порядка, который является невырожденным. Его порядок и называется рангом матрицы.

 

Определение. Порядок наибольшего невырожденного минора называется рангом матрицы.

Обозначается 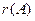. Примеры:

Матрица размера 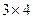ранга 2. 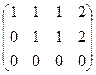. Здесь есть невырожденный минор порядка 2,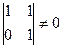

.

Миноры 3 порядка можно рассматривать не все, достаточно только окаймляющие, то есть содержащие уже найденный минор меньшего порядка.

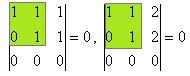
поэтому ранг не равен 3, а остаётся равен 2, так как минор 2 порядка уже найден. Миноров 4 порядка в этой матрице нет, так как всего 3 строки. Итак, 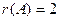. Цветом закрашен базисный минор.

 

Ранг прямоугольной матрицы размера 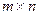меньше или равен, чем минимальное из чисел m, n. Причина: минор более высокого порядка в этой матрице просто не существует, ведь размер вписанного квадрата не может превышать ни длину, ни ширину прямоугольника, в который вписан этот квадрат.

 

Пример. Матрица ранга 1. Здесь все строки пропорциональны 1-й.

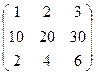
Матрица А является матрицей ранга 0 она состоит только из нулей (очевидно, что если в матрице есть хоть один элемент, не равный 0, то он уже является минором 1 порядка, то есть ранг не 0, а уже 1).