2017-10-25
418
В общем случае, основная матрица системы не квадратная, а прямоугольная. При этом базисный минор порядка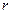 
, где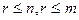 
. Возможно, что ранг даже и строго меньше, 
.
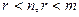Если ранг основной матрицы меньше, чем число неизвестных, т.е.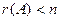 
, то система неопределённая, так как есть столбцы, не входящие в базисный минор, эти неизвестные переносятся вправо.
Если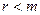 
(ранг меньше числа неизвестных) то в процессе преобразований методом Гаусса получатся 
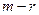строк, состоящих из нулей. Уравнения, соответствующие им, в системе уравнений не несут никакой информации: 
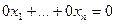. Такие уравнения просто вычёркиваются.
А если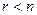 
т.е. ранг меньше числа неизвестных (то есть базисный минор не заполняет всю матрицу до правого края), 
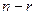переменных нужно перенести вправо в каждом уравнении (они называются свободными переменными), а 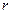базисных переменных оставить слева. Фактически, при этих действиях мы стремимся к тому, чтобы слева получить именно квадратную матрицу (порядка 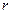), причём она уже будет приведена к треугольному виду, и можно будет выражать неизвестные 
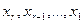поочерёдно. Но в отличие от определённых систем, справа в это время не просто константы, а блоки, состоящие из констант и свободных неизвестных. Итак, 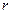переменных будут не конкретными числами, а функциями от последних 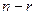переменных. Совокупность таких выражений называется ОБЩИМ РЕШЕНИЕМ.
Если присвоить какие-либо значения свободным переменным и вычислить 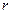базисных, то получим тогда уже конкретный набор из n чисел, это называется ЧАСТНЫМ РЕШЕНИЕМ. Частных решений может быть бесконечно много, потому что присваивать свободным неизвестным можно любые действительные значения.
Общее и частное решение.
Пример.
Решить систему уравнений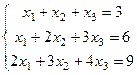 
.
Запишем расширенную матрицу и преобразуем её методом Гаусса:
.
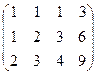
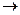
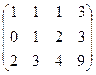
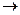
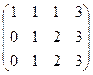
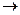
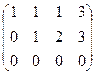Из 2-й строки отняли 1-ю, из 3-й удвоенную 1-ю. Замечаем, что 2 и 3 строка одинаковы, вычитаем из 3-й 2-ю, и 3-я строка получилась состоящей из 0. Это уравнение 0 = 0, очевидно, его можно вычеркнуть. Базисный минор 2 порядка можно найти в левом верхнем углу. Здесь m = 3, n = 4, r = 2.
Обратите внимание. Типичной и характерной ошибкой является то, что вычёркивают обе пропорциональных строки, а не одну. Но если провести алгоритм Гаусса до конца, то видно, что одна из них остаётся и несёт содержательную информацию, а её копия лишняя, она обратилась в 0. Не нужно торопиться и вычёркивать все пропорциональные строки, ведь хотя бы одна из них не лишняя!
Развернём две оставшихся строки снова в систему уравнений:
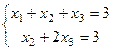
Здесь перенесём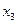 
вправо, 3-я переменная - свободная, базисный минор в левом углу. Замечание. Впрочем, это не единственный вариант: базисный минор можно составить из фрагментов 1 и 3 столбца, тогда 
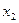была бы свободная. Итак, перенесём :
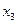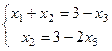Основная матрица системы фактически стала квадратной, 2 порядка, т.е. множество коэффициентов при базисных переменных образует такую квадратную матрицу: 
.
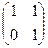Просто справа при этом не только константы, а составные выражения из констант и каких-то параметров. Видно, что 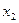уже и так выражена, 
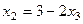. Подставим это выражение в 1-е уравнение, чтобы выразить отдельно 
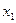через .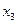
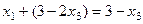в итоге 
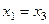. Итак, 
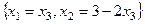- общее решение. В нём есть один свободный параметр .
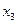Его можно записать также и в виде такого вектора: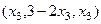 
.
Если задавать любое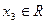 
, будет получать тройки чисел, которые служат частными решениями.
Например, при 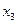= 1 получим (1,1,1). При 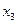= 0 получим (0,3,0). Частных решений бесконечно много.
* Свободных неизвестных 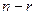. Как правило, это последние, но не факт: всё зависит от строения системы. Если, например, 2-й столбец кратен первому, то базисный минор не удастся выбрать в левом верхнем углу, а только с разрывом через второй столбец, тогда 2-й столбец не будет базисным, тогда 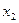- свободная пременная, а не базисная.
