Строение матрицы линейного оператора

Докажем, что образы базисных векторов расположены в столбцах матрицы, что именно при таком строении матрицы умножение её на вектор-столбец будет задано корректно, то есть оно будет действительно отображать базисные векторы в их образы.

Умножим произвольную квадратную матрицу на и : , .

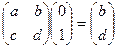Базисные векторы при умножении на квадратную матрицу отобажаются именно в такие векторы, координаты которых записаны в 1 и 2 столбце матрицы. Строение матрицы оператора: столбцы есть образы базисных векторов при данном отображении, то есть столбец номер 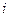матрицы оператора содержит вектор .

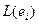Итак, если задан какой-либо закон, по которому отображаются векторы, то чтобы задать матрицу оператора, надо найти, куда отображаются базисные векторы. Для примера, найдём матрицу оператора поворота на произвольный угол .

Расстояния r1 и r2 здесь равны и . Красным показаны образы базисных векторов. Получаем матрицу .

При получится 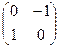Действие оператора на любой вектор задаётся матрицей так: 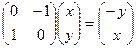- любой вектор поворачивается на 90 градусов.

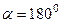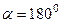При матрица будет иметь вид , и действительно, умножение на такую матрицу переводит любой вектор в , а при повороте на каждый вектор как раз и должен повернуться и стать противоположным исходному.

Оператор проекции пространства на плоскость.

Базисные векторы (1,0,0) и (0,1,0) остаются на своём месте, а (0,0,1) отображается в (0,0,0).

Матрица оператора проекции:

Каждый вектор 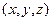он отображает в :

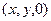Здесь естественным образом возникает такое понятие как ядро линейного оператора.Множество векторов, которые отображаются в 0, называется ядром оператора. .

Для примера выше (проекции) ядро - это ось .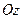

Тождественный оператор. Линейный оператор, который отображает каждый вектор в исходный, называется тождественным. I(x)=x. Ему соответствует матрица Е.

Композиция операторов. Если последовательно действуют два линейных оператора: то итоговое отображение называется композицией двух операторов. Соответственно, с помозью матриц это задаётся так: 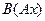, что равно , так что композиции операторов соответствует произведение матриц.

Обратный оператор.

Определение. Если для линейного оператора L существует линейный оператор , который каждый вектор отображает обратно: , т.е. в композиции с исходным получится тождественный оператор тогда L называется обратимым, а обратным для L.

Примеры: поворот на угол - обратимый, проекция - необратимый линейный оператор. Обратному оператору соответствует обратная матрица.

Свойство. Линейный оператор является обратимым .

Собственные векторы.

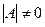Определение. Если для ненулевого вектора выполняется , то 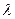называется собственным числом, а вектор 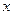называется собственным вектором, соответствующим этому собственному числу.

Геометрически это означает, что при действии отображения вектор остаётся на той же самой прямой. Для нулевого вектора рассматривать это понятие нет смысла, ведь 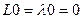для любого числа .

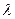Не для каждого оператора существуют собственные векторы. Так, при повороте плоскости на произвольный угол (кроме 0 и 180⁰) ни один вектор не остаётся на той же самой прямой. При вращении шара в пространстве: все векторы на оси вращения - собственные, они соответствуют .

Если растяжение по оси x с коэффициентом 2, а по оси y с коэффициентом 3, то векторы, не лежащие на осях, поворачиваются, и они не являются собственными.

Теорема 1. Линейная комбинация собственных векторов, соответствующих одному и тому же числу 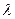, тоже является собственным вектором, соответствующим .

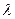Доказательство. Дано , . Тогда = .

Итак, для линейной комбинации, действие оператора тоже равносильно умножению на 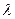, что и требовалось доказать.

Следствия: Если какой-то вектор на прямой является собственным, то и любой другой вектор на этой же прямой является собственным, так как он кратен первом у вектору, то есть является его линейной комбинацией. Если растяжение в плоскости на один и тот же коэффициент по двум осям, то и все векторы плоскости - собственные векторы.

Теорема 2. Любые два собственных вектора, соответствующих различным собственным числам, образуют ЛНС (линейно-независимую систему).

Доказательство. Дано , 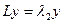. Допустим, что они были бы линейно-зависимы, то есть предположим .

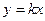Можно сначала отобразить линейным оператором, а потом представить в виде 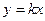, а можно наоборот, сначала выразить через , а потом применить отображение:

тогда , то есть . Но вектор 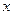ненулевой, коэффициент тоже. Тогда , то есть 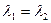, а это противоречит условию теоремы. Итак, предположение 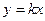ложно, векторы не могут быть линейно-зависимы. Что и требовалось доказать.

Вывод: Вся прямая состоит из собственных векторов, соответствующих одному и тому же 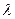, там не может быть векторов, соответствующих другим числам, а также векторов, не являющихся собственными.

Теорема 3. Если 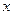является собственным вектором линейного оператора 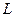, соответствующим 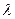, то он также является собственным и для обратного оператора , и соответствует числу .

Доказательство. Если , то по определению обратного оператора . Но тогда вынесем константу:

а значит, .

Введём такие понятия: Характеристическая матрица .

Характеристическое уравнение: (вычислить определитель хар. матрицы и приравнять к 0).

Теорема 4. Число 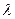является собственным для линейного оператора, заданного матрицей 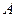, тогда и только тогда, когда .

Доказательство. Покажем для матрицы 2 порядка. Запишем подробно выражение :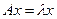

, тогда

Это кажется похоже не неодородную, но на самом деле это однородная система, так как справа не константы, а выражения с теми же переменными, что и слева, то есть их можно перенести все в одну сторону, и справа останутся 0, вот что получилось:

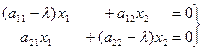
Если основная матрица такой системы невырождена, то решение только тривиальное (так как ранг равен числу переменных, и нет свободных переменных), а если вырождена, то нетривиальные решения есть.

Итак, решение существует , это и есть , так как это определитель матрицы .

Что и требовалось доказать.