Линейный оператор и его матрица
В этой главе будут изучаться отображения векторных пространств.
Вспомним, что при умножении квадратной матрицы на столбец, один вектор преобразуется в другой. Получается, что квадратная матрица задаёт некоторое отображение одних векторов в другие, то есть выступает в роли функции.
Определение. Отображение 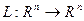 называется линейным отображением (синоним: линейный оператор) если выполнены 2 условия:
называется линейным отображением (синоним: линейный оператор) если выполнены 2 условия:
1) 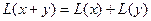 2)
2) 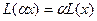 .
.
Умножение квадратной матрицы на вектор удовлетворяет свойствам линейности, в силу свойств умножения матриц.
Из определения напрямую следует, что всякое линейное отображение зависит только от того, куда отображаются базисные векторы: 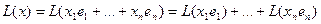 =
= 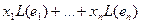 .
.
Образ вектора x в итоге зависит от координат вектора x и от образов базисных векторов, то есть линейный оператор однозначно задаётся образами базисных векторов.
Докажем ещё такое свойство: L(0)=0.
Пусть 0 вектор задан в виде 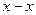 . Тогда:
. Тогда: 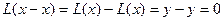 .
.
 2017-10-25
2017-10-25 414
414








