2017-10-25
374
Любой вектор можно выразить не только как комбинацию базисных векторов, расположенных на осях, например (1,0) и (0,1), но и как комбинацию какой-то другой линейно-независимой системы.
Так, 
, в ведь то же время и 
.
В декартовом базисе координаты (3,2) (пройти 3 шага вправо и 2 вверх), а в новом базисе, состоящем из векторов (1,1) и (1,0) координаты (2,1) (пройти 2 шага по диагонали и 1 шаг вправо).
Найти новые координаты можно так. Запишем их сначала как неизвестные в векторном равенстве:
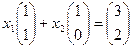а это очевидно, преобразуется к системе: 
. Ответ: координаты (2,1).
Матрица, где векторы нового базиса записаны по столбцам, а именно 
для этого примера, называется матрицей перехода от старого к новому базису, обозначается 
. Именно она и есть основная матрица системы, которую надо решить. Правая часть это старые координаты. Верно равенство 
, т.е. новые координаты можно найти и так: 
умножив обратную матрицу на старые координаты. Впрочем, это то же самое, что решить систему с квадратной матрицей матричным методом.
