Перпендикулярность прямой и плоскости

Прямая перпендикулярна плоскости, если она перпендикулярна двум прямым этой плоскости, например, её горизонтали и фронтали. Построение перпендикуляра начинают с построения горизонтали и фронтали плоскости (см. рис. 29–36).

Затем к этим прямым проводят перпендикуляр так, как это сделано на примере рисунка 41 а: пусть задана фронталь f. Требуется из точки А опустить на фронталь перпендикуляр n (ранее мы рассматривали эту задачу, но для закрепления материала при переходе к перпендикулярности прямой и плоскости, напомним ещё раз).

Рис. 41 а. Рис. 41 б

На основании свойства 8 ортогонального проецирования прямой угол проецируется без искажения, если одна из его сторон – линия уровня.. Следовательно, прямой угол между f и n проецируется на в натуральную величину: , так как параллельна . Точка – основание перпендикуляра. Горизонтальная проекция перпендикуляра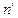

определяется положением точек и .

Аналогично строится перпендикуляр m к горизонтали h (рис. 41 б).

Прямая n (рис. 42) перпендикулярна плоскости (АВС), так как n 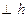и (на основании свойства 8 ортогонального проецирования).

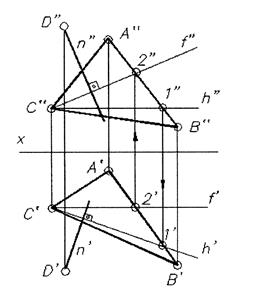
Рис. 42

При построении на комплексном чертеже перпендикуляра к плоскости надо иметь в виду: если , то фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции фронтали (), а его горизонтальная проекция– горизонтальной проекции горизонтали ().

Приведенное решение используется при определении расстояния от точки до прямой частного положения, например, горизонтали.

Пример: Определить расстояние от точки С до прямой АВ (рис. 42.1.).

Рис. 42.1.

Решение. Расстояние от точки до прямой измеряется натуральной величиной отрезка перпендикуляра, опущенного на неё из этой точки. Поскольку данная прямая – горизонталь, то в соответствии со свойством 8 проецирования прямого угла горизонтальная проекция перпендикуляра перпендикулярна горизонтальной проекции горизонтали. Проводим перпендикуляр из к и затем строим на его горизонтальной проекции вспомогательный прямоугольный треугольник для определения натуральной величины отрезка перпендикуляра СК, т.е. – (рис. 42.1.).