2017-10-25
572
Две плоскости взаимно перпендикулярны, если одна из них содержит прямую, перпендикулярную к другой плоскости. Поэтому построение перпендикулярных плоскостей сводится к построению взаимно перпендикулярных прямой и плоскости.
Пример 1. Провести через прямую а плоскость, перпендикулярную другой плоскости.
Решение. На рис. 42.2. рассмотрена задача по проведению через прямую а плоскости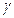 
, перпендикулярной плоскости 
(АВС). Задача сводится к предыдущей, если на прямой а задать точку D и провести через неё перпендикуляр n к плоскости . Поскольку плоскость 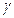образована двумя пересекающимися прямыми, одна из которых перпендикулярна , то, как известно, плоскость, содержащая перпендикуляр к другой плоскости, сама перпендикулярна этой плоскости.
Рис. 42.2.
Пример 2. Плоскость задана следами 
и 
. Построить плоскость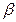 
, перпендикулярную заданной. Плоскость 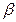задать пересекающимися прямыми. (рис. 42.3.).
Рис. 42.3.
Решение. Проводим прямую l, перпендикулярную плоскости , т.е. 
и 
. Затем заключаем эту прямую l в какую-либо плоскость. Последняя будет искомой. В данном случае плоскость 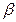задана двумя пересекающимися прямыми m (произвольная прямая) и l.
