Пересечение прямой с плоскостью

Для определения точки пересечения прямой m с плоскостью (АВС) выполняют следующие операции.

1. Через прямую m проводят вспомогательную проецирующую плоскость 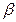(рис. 39). В данном примере проводим горизонтально проецирующую плоскость .

Условие задачи Решение

Рис. 39

2. Определяют линию пересечения n плоскости 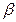с плоскостью (АВС). На рис. 39 горизонтальная проекция этой линии 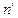совпадает с 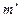по построению, а фронтальная 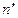определяется проецированием точек и на фронтальные проекции и сторон треугольника АВС.

3. Находят точку К пересечения прямой m с плоскостью . Фронтальная проекция 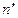линии пересечения пересекает 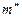в точке . Поскольку лежит в плоскости , то К принадлежит как плоскости , так и прямой 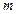, т.е. является точкой их пересечения. Её горизонтальная проекция определяется проецированием на .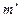

Видимость прямой и плоскости относительно горизонтальной плоскости проекций определяется с помощью горизонтально проецирующих точек 2 и 3. Точка 2 лежит на АС, а 3 – на m. Их фронтальные проекции и показывают, что точка 2 находится ниже точки 3 и поэтому на горизонтальной плоскости проекций горизонтальная проекция точки 2 будет закрыта проекцией 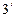точки 3. Отсюда следует, что проекция стороны АС расположена ниже проекции 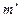и участок этой прямой с левой стороны до будет видимым.

Относительную видимость на фронтальной плоскости проекций можно определить с помощью фронтально конкурирующих точек 4 и 5. Как показывают горизонтальные проекции этих точек 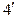и , точка 4 лежит ближе к наблюдателю, чем точка 5, но поскольку последняя принадлежит прямой m, то участок её фронтальной проекции невидим.

На рис. 40 дан пример построения точки пересечения прямой АВ с плоскостью общего положения , заданной следами.

Рис. 40

В данном случае через прямую АВ проведена горизонтально проектирующая плоскость 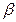. На горизонтальной плоскости проекций линия пересечения MN плоскостей совпадает с горизонтальным следом этой плоскости. Построив фронтальную проекцию прямой , находим фронтальную проекцию точки пересечения её с прямой АВ – .

Теперь по линии связи находим горизонтальную проекцию точки . В завершении определяем видимость прямой АВ относительно точки пересечения (рис. 40).

При нахождении точки встречи прямой с горизонтально проектирующей (или фронтально-проектирующей) плоскостью решение задачи значительно упрощается[4].

Покажем это на примере: найдем точку встречи прямой с горизонтально-проектирующей плоскостью 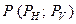(см. рис. 54).

Рис. 54 Рис. 55

Точка встречи К прямой АВ с плоскостью Р – это точка, общая для прямой и плоскости. Поскольку эта точка лежит на прямой АВ, её горизонтальная проекция k должна лежать на горизонтальной проекции ab прямой АВ. Поскольку же эта точка лежит и в горизонтально-проектирующей плоскости Р, то её горизонтальная проекция k должна лежать на горизонтальном следе этой плоскости .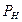

Следовательно, горизонтальная проекция k искомой точки определяется на пресечении горизонтальной проекции ab прямой с горизонтальным следом 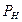(рис. 55).

Фронтальная проекция точки встречи К определяется на фронтальной проекции прямой 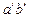линией проекционной связи вверх от точки 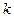(см. рис. 55).