Решение задач способом перемены одной плоскости проекций

Задача 1. Найти расстояние от точки 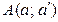до плоскости общего положения Р .

Для решения задачи способом перемены плоскости проекции, необходимо выбрать новую плоскость проекций, параллельную искомому расстоянию.

Следовательно, если выбирается новая плоскость проекций 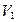, то на ортогональном чертеже новая ось 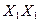[5] должна быть выбрана перпендикулярно к следу 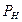. На рисунке 78 проведена новая ось проекций 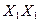перпендикулярно к следу 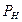и построен новый след 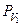, а также новая проекция точки .

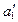Рис. 78 Рис. 79

В результате перемены плоскости проекций V на 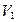, плоскость общего положения Р, заданная в системе 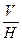, оказалась плоскостью фронтально-проектирующей в системе .

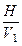Из точки 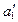опускаем перпендикуляр на след 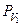и отмечаем точку 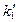его пересечения с этим следом (см. рис. 79): отрезок 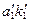будет являться проекцией искомого расстояния на плоскость 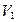. Длина же проекции 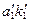равна искомому расстоянию, т.к. плоскость 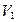была выбрана параллельно этому расстоянию.

Для построения проекции 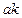искомого расстояния на плоскость Н через точку 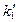проведена линия проекционной связи, перпендикулярная к оси 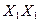, а через точку а – прямая, перпендикулярная к следу 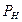: взаимное пересечение указанных прямых определяет точку k (рис. 79).