2017-10-25
379
Решение метрических[10] задач на ортогональном чертеже значительно упрощается путем изменения положения в пространстве одной или двух плоскостей проекций.
Сущность способа заключается в том, что пространственное положение объекта не изменяют, а вводят новую дополнительную плоскость проекций, расположенную таким образом, чтобы интересующие нас объекты проецировались на неё в удобном для решения задачи положении. При этом новая плоскость проекций должна быть перпендикулярна к одной из имеющихся плоскостей проекций.
Введем, например, в систему плоскостей проекций 
новую плоскость проекций 
(рис. 75.1). В результате будем иметь другую систему проекций 
. Новая и старая система плоскостей проекций имеют общую, связывающую их плоскость проекций 
. Новой осью проекций будет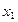 
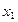. Теперь каждая точка пространства, например, точка В проецируется на три попарно перпендикулярные плоскости, причем координата Z точки В в плоскостях и будет одна и та же. Для получения плоского чертежа сначала совмещают плоскость с плоскостью , вращая вокруг оси , а затем полученный плоский чертеж поворотом вокруг оси х совмещают с плоскостью 
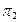(рис. 75.2).
|
|
|
Рис. 75.1
Рис. 75.2
Примером использования этого метода может служить задача на определение расстояния от точки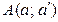 
до фронтально-проектирующей плоскости 
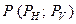(рис. 76).
Рис. 76 Рис. 77
Для решения задачи опустим из точки А перпендикуляр на плоскость Р и найдем точку встречи 
этого перпендикуляра с данной плоскостью: отрезок АК будет являться искомым расстоянием. На рисунке 77 эти построения выполнены: фронтальная проекция 
отрезка перпендикуляра является его истинной длиной, т.к. в пространстве отрезок АК параллелен фронтальной плоскости проекций, что следует из параллельности его горизонтальной проекции ak оси ОХ.
Сравнивая только что выполненное решение с приведенным ранее на рисунках 72-75, становится очевидным, что решение аналогичной задачи (и им подобных) упрощается, если путем изменения положения одной или двух плоскостей проекций, мы в результате вместо заданной плоскости общего положения Р 
заданной в системе 
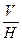(рис. 72), преобразуем её в плоскость частного положения (горизонтально-проектирующую) в системе 
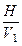(рис. 79).
Такую перемену плоскости проекций, соответствующая преобразованию плоскости Р общего положения в горизонтально-проектирующую.для упрощения решения задачи нахождения расстояния от заданной точки А до плоскости Р покажем на рисунках 78-79.
