Взаимное пересечение плоских фигур

Линия пересечения двух плоских треугольников определяется двумя точками, общими для этих треугольников. Такие две точки легко могут быть найдены, как точки пересечения двух любых сторон одного треугольника с плоскостью второго треугольника.

Найдем линию пересечения заданных треугольников и 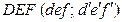(рис. 69).

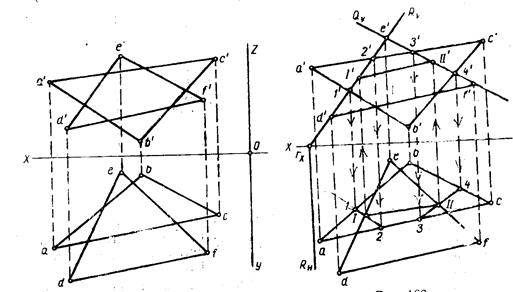
Рис. 69 Рис. 70

На рисунке 70 показано построение линии пересечения этих треугольников: определены точки встречи и пересечения сторон и треугольника DEF с плоскостью треугольника АВС: эти точки и определяют искомую линию пересечения.

Для построения точки I встречи прямой DE c плоскостью АВС через прямую DE проведем вспомогательную фронтально-проектирующую плоскость и построим прямую 1–2 пересечения этих плоскостей. На пересечении горизонтальных проекций 1–2 и de определена горизонтальная проекция I точки встречи, фронтальная проекция построена на фронтальной проекции 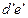прямой (см. рис. 70).

Для построения точки II встречи прямой EF с плоскостью АВС через эту прямую проведем вспомогательную фронтально-проектирующую плоскость Q, фронтальный след 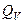которой проходит через фронтальную проекцию прямой (горизонтальный след 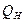плоскости Q на рисунке 70 не показан, т.к. его наличие не является необходимым для решения задачи). Построена прямая 3–4 пересечения плоскостей Q и АВС, и на пересечении этой прямой с прямой EF определена точка II: первоначально определена горизонтальная проекция II этой точки на пересечении горизонтальных проекций 3–4 и ef, а затем фронтальная проекция на фронтальной проекции .

Рис. 71

На рисунке 71 показано определение видимости пересекающихся фигур. Пользуясь конкурирующими точками 4 и IV, определена видимость на плоскости V, а пользуясь точками 5 и V – на плоскости Н.