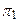 , ,  , , 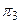 – горизонтальная, фронтальная и профильная плоскости проекции.
x, y, z – оси проекций (абсцисс, ординат и аппликат).
A, B, C, D, 1, 2, 3, 4 … – точки в пространстве.
A¢, B¢, C¢, D¢, 1¢, 2¢, 3¢, 4¢ … – горизонтальные проекции точек.
A¢¢, B¢¢, C¢¢, D¢¢, 1¢¢, 2¢¢, 3¢¢, 4¢¢ … – фронтальные проекции точек.
A¢¢¢, B¢¢¢, C¢¢¢, D¢¢¢, 1¢¢¢, 2¢¢¢, 3¢¢¢, 4¢¢¢ … – профильные проекции точек.
a, b, c, l – линии в пространстве.
a¢, b¢, c¢ – горизонтальные проекции линий.
a¢¢, b¢¢, c¢¢ – фронтальные проекции линий.
a¢¢¢, b¢¢¢, c¢¢¢ – профильные проекции линий. – горизонтальная, фронтальная и профильная плоскости проекции.
x, y, z – оси проекций (абсцисс, ординат и аппликат).
A, B, C, D, 1, 2, 3, 4 … – точки в пространстве.
A¢, B¢, C¢, D¢, 1¢, 2¢, 3¢, 4¢ … – горизонтальные проекции точек.
A¢¢, B¢¢, C¢¢, D¢¢, 1¢¢, 2¢¢, 3¢¢, 4¢¢ … – фронтальные проекции точек.
A¢¢¢, B¢¢¢, C¢¢¢, D¢¢¢, 1¢¢¢, 2¢¢¢, 3¢¢¢, 4¢¢¢ … – профильные проекции точек.
a, b, c, l – линии в пространстве.
a¢, b¢, c¢ – горизонтальные проекции линий.
a¢¢, b¢¢, c¢¢ – фронтальные проекции линий.
a¢¢¢, b¢¢¢, c¢¢¢ – профильные проекции линий.
 , , 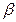 , , 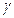 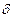 – плоскости в пространстве. – плоскости в пространстве.
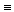 – совпадение. – совпадение.
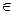 – принадлежность для точки. – принадлежность для точки.
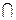 – линия пересечения плоскостей (напр. плоскостей проекций) – линия пересечения плоскостей (напр. плоскостей проекций)  или точка пересечения линий (напр.линий проекций связей). или точка пересечения линий (напр.линий проекций связей).
|
СЛЕДЫ ПРЯМОЙ ЛИНИИ
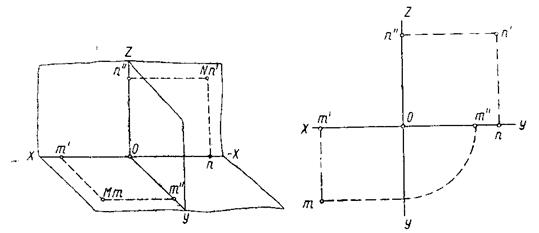
Рис. 9 Рис. 10
На рисунке 9 наглядно и на рисунке 10 ортогонально изображены две точки – М и N, причем, точка М лежит в плоскости Н, а точка N – в плоскости V.
Эти две точки определяют некоторую прямую, которая показана на рисунках 11 и 12, где точки М и N, а также их одноименные проекции соединены прямыми линиями.
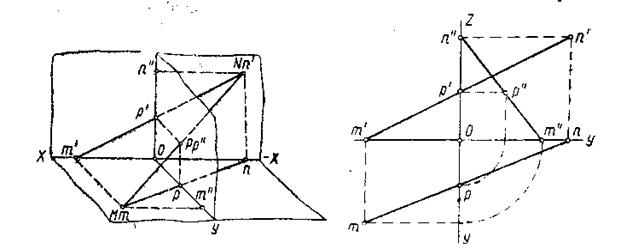
Рис. 11 Рис. 12
Построенная прямая проходит из первого угла пространства в пятый и, следовательно, пересекает профильную плоскость W в некоторой точке, например, Р, построение которой показано на этих рисунках.
Если на прямой MN выбрать две произвольные точки А и В (Рис. 13 и 14), то можно сказать, что эти точки определяют некоторую прямую АВ, для которой точка М является следом на плоскости Н – горизонтальным следом; точка N – следом на плоскости V, или фронтальным следом и точка Р – следом на плоскости W, или профильным следом.
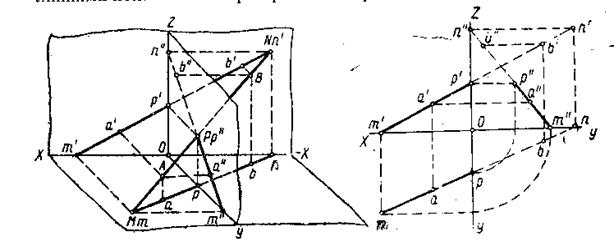
Рис. 13 Рис. 14
Охарактеризуем местоположение каждой проекции каждого из трех следов прямой АВ на ортогональном чертеже (Рис. 14):
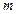 – горизонтальная проекция горизонтального следа прямой лежит на горизонтальной проекции
– горизонтальная проекция горизонтального следа прямой лежит на горизонтальной проекции 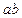 прямой;
прямой;
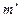 – фронтальная проекция горизонтального следа прямой определяется на пересечении фронтальной проекции
– фронтальная проекция горизонтального следа прямой определяется на пересечении фронтальной проекции 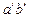 прямой с осью ОХ;
прямой с осью ОХ;
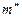 – профильная проекция горизонтального следа прямой определяется на пересечении профильной проекции
– профильная проекция горизонтального следа прямой определяется на пересечении профильной проекции  прямой с осью OY $
прямой с осью OY $
n – горизонтальная проекция фронтального следа прямой определяется на пересечении горизонтальной проекции 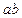 прямой с осью ОХ;
прямой с осью ОХ;
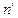 – фронтальная проекция фронтального следа прямой лежит на фронтальной проекции
– фронтальная проекция фронтального следа прямой лежит на фронтальной проекции 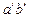 прямой;
прямой;
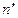 – профильная проекция фронтального следа прямой определяется на пересечении профильной проекции
– профильная проекция фронтального следа прямой определяется на пересечении профильной проекции  прямой с осью OZ;
прямой с осью OZ;
р – горизонтальная проекция профильного следа прямой определяется на пересечении горизонтальной проекции 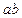 прямой с осью OY;
прямой с осью OY;
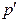 – фронтальная проекция профильного следа прямой определяется на пересечении фронтальной проекции
– фронтальная проекция профильного следа прямой определяется на пересечении фронтальной проекции 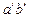 прямой с осью OZ;
прямой с осью OZ;
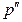 – профильная проекция фронтального следа прямой лежит на профильной проекции прямой.
– профильная проекция фронтального следа прямой лежит на профильной проекции прямой.
Руководствуясь этим местоположений отдельных точек, легко решаются задачи на построение следов заданной прямой в ортогональной плоскости.
 2017-10-25
2017-10-25 310
310








