2017-10-25
390
Линией пересечения двух плоскостей является прямая, все точки которой принадлежат обеим плоскостям. Для определения этой линии в общем случае необходимо найти две точки, каждая из которых принадлежит двум данным плоскостям.
1. Пересекаются две плоскости P и Q, у которых пересекаются одноименные следы (Рис. 39).
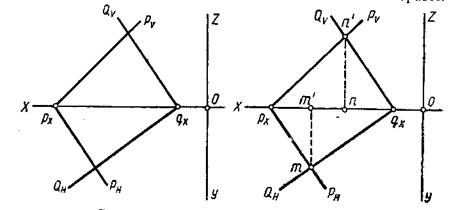
Рис. 39 Рис. 40
Точки пересечения одноименных следов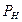 
и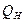 
, а также 
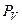и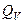 
– точки М 
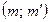и N 
– являются точками общими для данных плоскостей (Рис. 40).
Эти точки определяют линию пересечения данных плоскостей – прямую MN, проекции линии пересечения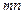 
–– горизонтальная и 
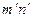–– фронтальная – определяются путем соединения прямыми одноименных проекций отмеченных точек (Рис. 40).
На рисунке 41 показано пересечение плоскости общего положения Р с горизонтально-проектирующей плоскостью Q: последовательность построения линии пересечения плоскостей как в предыдущей задаче только с учетом, что горизонтальная проекция линии пересечения в данном случае совпадает с горизонтальным следом 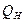, т.к. плоскость Q – горизонтально-проектирующая.
|
|
|
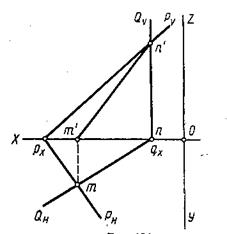
Рис. 41
2. У пересекающихся плоскостей на одной плоскости проекций следы параллельны (рис. 42).
На рисунке 42 изображены плоскости P и Q, у которых горизонтальные следы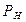 
и 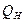параллельны. Точка пересечения фронтальных следов 
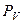и 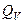определяет одну общую точку для данных плоскостей – точку 
.
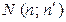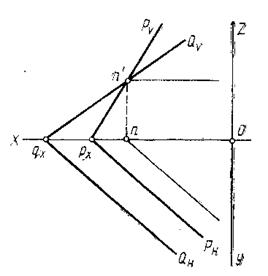
Рис. 42
Параллельность горизонтальных следов показывает, что линия пересечения плоскостей в горизонтальной плоскости Н должна быть параллельной этим следам, т.е. является общей горизонталью данных плоскостей и её фронтальная проекция параллельна оси ОХ, а горизонтальная – горизонтальным следам заданных плоскостей.
