Прямая линия однозначно определяется двумя точками (например А и В). На рисунке 5 построенына плоскостях проекций 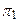 ,
,  и
и 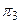 три проекции прямой линии АВ:
три проекции прямой линии АВ: 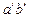 ,
,  и
и  .
.

Рис. 5 Рис. 6
На рисунке 6 та же прямая АВ представлена проекциями 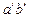 ,
,  и
и  на ортогональном чертеже.
на ортогональном чертеже.
Если на прямой АВ взять некоторую точку С и построить её проекцию 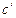 на горизонтальную плоскость
на горизонтальную плоскость 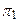 , то она будет лежать на прямой
, то она будет лежать на прямой 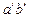 (см. рис. 5).
(см. рис. 5).
Аналогичным образом фронтальная проекция  будет лежать на проекции
будет лежать на проекции  , а профильная –
, а профильная –  на проекции
на проекции  (Рис. 6), т.е. если точка лежит на прямой, то её проекции лежат на одноимённых проекциях этой прямой.
(Рис. 6), т.е. если точка лежит на прямой, то её проекции лежат на одноимённых проекциях этой прямой.
Точка С разделила отрезок АВ в некотором отношении  . В таком же отношении точка
. В таком же отношении точка 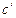 разделила отрезок
разделила отрезок 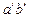 ; точка
; точка  – отрезок
– отрезок  и, наконец, точка
и, наконец, точка  – отрезок
– отрезок  , т.е.
, т.е.  . Отсюда следует, что если точка делит отрезок прямой в данном отношении, то проекции этой точки делят одноименные проекции отрезка в том же отношении.
. Отсюда следует, что если точка делит отрезок прямой в данном отношении, то проекции этой точки делят одноименные проекции отрезка в том же отношении.
Точки пересечения прямой с плоскостями проекций называют следами.
ВЫНЕСТИ В КОНЕЦ?

Рис. 1.1. Рис. 2.1.
Представим в пространстве три взаимно-перпендикулярные плоскости проекций: го-
ризонтальную – 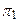 (H ), вертикальную (фронтальную) –
(H ), вертикальную (фронтальную) –  (V) ипрофильную –
(V) ипрофильную – 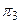 (W) (Рис. 1).
(W) (Рис. 1).
Плоскости 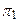 и
и  пересекаются по оси проекции ОХ; плоскости
пересекаются по оси проекции ОХ; плоскости 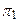 и
и 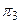 – по оси OY иплоскости
– по оси OY иплоскости  и
и 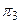 – по оси OZ.
– по оси OZ.
Возьмем в этом квадрате точку А и спроектируем её ортогонально на указанные плоскости: горизонтальная проекция точки  будет –
будет –  , фронтальная проекция –
, фронтальная проекция –  и профильная –
и профильная –  (Рис. 1, 2).
(Рис. 1, 2).
Отрезки  ,
,  и
и  выражают расстояния от точки А до каждой из плоскостей проекций; эти отрезки называются прямоугольными координатами точки А и обозначаются соответственно.
выражают расстояния от точки А до каждой из плоскостей проекций; эти отрезки называются прямоугольными координатами точки А и обозначаются соответственно.  (рис. 1.1.).
(рис. 1.1.).
Таким образом: три прямоугольные координаты точки однозначно определяют её положение в пространстве. Для точки А это условие сокращенно может быть записано в такой форме:  .
.
На рисунке 1 проекции точки А построена на трех взаимно перпендикулярных плоскостях. Практически же проекции точки строятся в одной плоскости.
Чтобы получить все три проекции точки в одной плоскости чертежа, нужно с плоскостью чертежа совместить все три плоскости 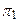 ,
,  и
и 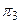 . Это совмещение выполняется следующим образом: плоскость
. Это совмещение выполняется следующим образом: плоскость  непосредственно совмещается с плоскостью чертежа (остается на месте); плоскость
непосредственно совмещается с плоскостью чертежа (остается на месте); плоскость 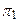 совмещается с плоскостью
совмещается с плоскостью  чертежа вращением по оси ОХ сверху вниз и плоскость
чертежа вращением по оси ОХ сверху вниз и плоскость 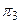 совмещается с плоскостью чертежа вращением вокруг оси OZ слева направо (см. рис. 2.1.).
совмещается с плоскостью чертежа вращением вокруг оси OZ слева направо (см. рис. 2.1.).
После этих преобразований ортогональные плоскости 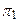 ,
,  и
и 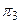 займут положение в одной плоскости чертежа (Рис. 2 и 3). Ось OУ (которая раньше была направлена на нас) в результате перемещений плоскостей
займут положение в одной плоскости чертежа (Рис. 2 и 3). Ось OУ (которая раньше была направлена на нас) в результате перемещений плоскостей 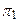 и
и 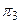 расслоилась на две составляющие:
расслоилась на две составляющие:  и
и  (правые нижние индексы
(правые нижние индексы 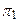 и
и 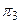 соответствуют тем плоскостям, при которых осталась ось Оу).
соответствуют тем плоскостям, при которых осталась ось Оу).
Проекция  точки А на горизонтальную плоскость
точки А на горизонтальную плоскость 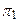 определяется двумя координатами: XА = ОaX и УА = ОaУ (см.рис. 3), что может быть записано так:
определяется двумя координатами: XА = ОaX и УА = ОaУ (см.рис. 3), что может быть записано так:  (X А; YА).
(X А; YА).
Проекция  точки А на фронтальную плоскость
точки А на фронтальную плоскость  определяется координатами: XА = ОaX и ZА = ОaZ, что тоже можно записать:
определяется координатами: XА = ОaX и ZА = ОaZ, что тоже можно записать:  (X А; ZА).
(X А; ZА).
Наконец, проекция  точки А на профильную плоскость
точки А на профильную плоскость 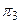 определяется тоже двумя координатами:
определяется тоже двумя координатами:  и
и  , т.е.:
, т.е.:  (Y А; ZА).
(Y А; ZА).
Мы видим, что любая из трех проекций точки А определяется по двум координатам,
 Рис. 3
Рис. 3
в то же время в координаты любых двух проекций входят три прямоугольные координаты однозначно определяющие её положение в пространстве.
 Рис. 4
Рис. 4
Таким образом очевидно, что по любым двум заданным проекциям точки можно построить третью.
Обратив внимание на расположение трех проекций точки А на ортогональном чертеже рис. 3, мы видим определенную закономерность: две проекции точки на две взаимно-перпендикулярные плоскости связаны прямой, перпендикулярной к линии пересечения плоскостей проекций.
Из этой закономерности для проверки правильности выполнения первого задания, (да и дальнейших тоже), необходимо помнить: горизонтальная  и фронтальная
и фронтальная  проекции точки лежат на одной вертикальной прямой, а фронтальная
проекции точки лежат на одной вертикальной прямой, а фронтальная  и профильная
и профильная  проекции точек лежат на одной горизонтальной прямой (рис. 2 и 3).
проекции точек лежат на одной горизонтальной прямой (рис. 2 и 3).
Линии, связывающие между собой проекции точки на ортогональном чертеже, называются линиями проекционной связи.
В объёмном отображении плоскости проекций 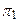 ,
,  и
и 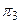 являются неограниченными поверхностями и при взаимном пересечении делят все пространство на восемь прямых трехгранных угла (Рис. 4).
являются неограниченными поверхностями и при взаимном пересечении делят все пространство на восемь прямых трехгранных угла (Рис. 4).
Положение точки в том или ином из восьми углов определяется не только величинами трех её координат, но и направлениями, по которым эти координаты должны откладываться: каждой из трех осей проекций дано два направления относительно начала координат 0: положительное и отрицательное (см. рис. 4).
 2017-10-25
2017-10-25 1119
1119
