Методы решения экономических задач. Прямые задачи. Обратные задачи

В повседневной практике управления современным предприятием используется огромное количество методов, на основании которых решаются экономические задачи: оптимизационные, имитационные, статистические, сетевые и т.д. Значительная часть задач экономической ориентации сводится либо к прямому счету (прямая задача), либо к обратному (обратные вычисления).

Прямые задачи – это констатирующие задачи, что означает следующее: заданы значения исходных показателей, на основании которых рассчитываются результирующие, что можно представить как

,

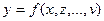где 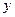- результирующий показатель;

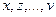- исходные показатели.

Примером прямой задачи может служить рентабельность, рассчитываемая на основании таких исходных показателей как: прибыль, основные и оборотные средства.

Задачи данного класса известны как транзакционные (OLTP - On-line Transaction Processing), то есть те, что предназначены для оперативной обработки данных.

Обратные вычисления, в отличие от задач прямого счета, предназначены для поиска тех значений исходных показателей, которые обеспечат желаемое значение результирующего. Искомыми величинами будут приросты (положительные или отрицательные) исходных показателей, то есть:

,

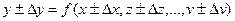где 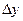- желаемый прирост результирующего показателя;

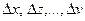- искомые приросты исходных показателей, которые могут быть как с положительными, так и с отрицательными знаками.

Примером обратной задачи может служить следующая постановка: известен уровень рентабельности предприятия в процентах, каковы должны быть прибыль, основные и оборотные средства, обеспечивающие повышение рентабельности на n%.

В практике управления задачи такого рода еще называют аналитическими (OLAP - On-line Analytical Processing). Они предназначены для подготовки информации в процессе формирования решений.

Цели решения прямых и обратных задач разные: прямые решаются для того, чтобы определить фактическое состояние предприятия, зависящее от его уже происшедших производственно-хозяйственных и финансовых операций), а аналитические (Как сделать чтобы?) - для того, чтобы сформировать управленческое решение.

Рассмотрим содержание этих задач на более детальном примере.

Расчеты в прямых задачах осуществляются на основании формул, используемых для определения фактического финансово-хозяйственного состояния предприятия (организации). Расчеты такого рода, как правило, особых сложностей не вызывают. Например, рентабельность, прибыль, затраты, оборотные и основные средства можно рассчитать на основании достаточно простых прямых формул, вид которых имеется в многочисленной литературе. Исходные данные для них находятся в бухгалтерской и другой отчетности.

Для указания правильной последовательности расчетов, можно воспользоваться ориентированным графом, узлы которого соотносятся с экономическими показателями, а дуги – указывают на последовательность их расчета. Допустим, в настоящее время руководство интересует фактическое состояние дел с прибылью, т.е. значения показателей от которых она зависит. Как правило, эти показатели характеризуют эффективность работы соответствующих структурных подразделений. Формулы, используемые при этом следующие:

,

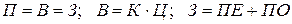где 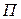- прибыль; 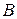- выручка; 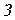- затраты; 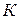- количество

продукции; 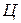- прежняя цена за единицу продукции; -

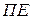переменные затраты; 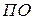- постоянные затраты.

Последовательность расчета прибыли представлена ориентированным графом (см. рис. 5.12).

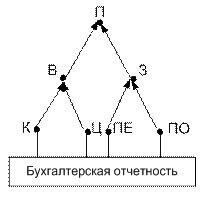
Рис. 5.12. Прямая задача.

Стрелки на рис. 5.12. указывают следующее: В - рассчитывается на основании показателе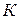й и 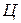, показатель 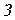на основани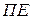и и 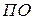, а показатель 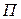с помощью 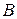и 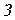. Источником данных служат формы бухгалтерской отчетности.

Обратная задача (как сделать чтобы?) решается с иной целью, которую в рамках рассматриваемого примера можно сформулировать следующим образом: необходимо определить такие значения показателе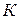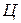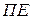й , , и 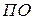, которые обеспечат изменение прибыли на заданную (желаемую) величину (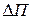). Для решения данной задачи граф показателей, приведенный на рис. 7.9, необходимо преобразовать в дерево целей (базу знаний), указав на нем дополнительную информацию. Дополнительная информация касается общей цели и подцелей: если значение показателя, отражающее уровень достижения цели должно увеличиваться, то рядом с соответствующим узлом графа указывается знак 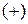, в противном случае 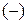. Обратимся к рис. 5.13, где представлена база знаний в виде дерева целей.

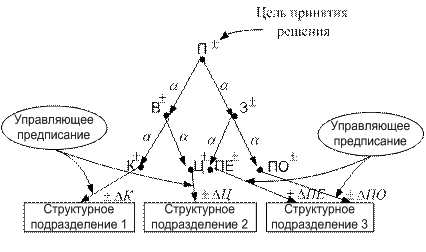
Рис. 5.13. Обратная задача.

Около всех показателей указаны знаки плюс или минус. Например, увеличение прибыли 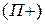следует достигать за счет увеличения выручки 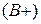и снижения затрат 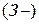. В свою очередь увеличение выручки следует достигать за счет увеличения количества 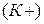и снижения продажной цены 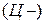, а снижения затрат 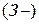за счет снижения постоянных 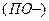и переменных 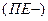затрат. Новые значения показателей (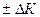, , 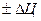, 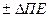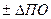), находящихся на нижнем уровне и направляемых в структурные подразделения, являются директивными. В другом периоде пути в достижении целей будут другие.

Одних направлений, в которых следует двигаться для того, чтобы достичь главной цели (увеличить прибыль) для построения дерева целей не достаточно. Необходимо тоже указать для каждого показателя приоритетность в достижении каждой подцели с помощью коэффициентов 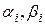. Сумма этих коэффициентов, касающаяся одного показателя должна быть равна единице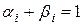

Обратная задача в данном конкретном случае формулируется следующим образом: фактический объем прибыли составил 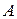единиц. Каковы должны быть показател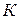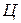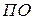и , , и 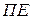, обеспечивающие рост прибыли на величину .

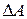Расчеты, как показано на рис. 7.10, выполняются сверху вниз: вначале следует отыскать положительный прирост выручки 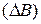и отрицательный для затрат 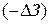, а затем положительный прирост количества 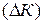и отрицательный для цены 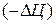, постоянных 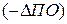и переменных затрат 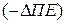. Для отыскания перечисленных приростов достаточно решить три системы линейных уравнений. Для составления первой, предварительно запишем:

;

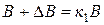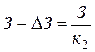
где 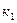, 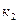- неизвестные коэффициенты, позволяющие рассчитать искомые приросты показателей.

Система уравнений для расчета 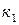и 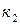примет вид:

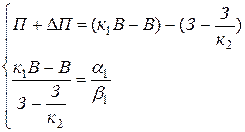
где 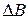и 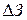- искомый прирост выручки, и искомое снижение затрат.

Решив данную систему, получим выражение для расчета коэффициентов 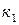и 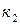. Они равны:

, .

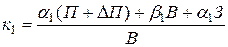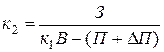Проверим правильность расчетов. Допустим, фактический объем прибыли составляет 5 ед. 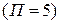, объем выручки 20 ед. 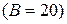, а затраты составили 15 ед. 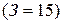. Пусть требуется повысить прибыль до 7 ед. 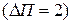. Если 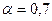, а 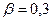, то применив полученные формулы получим: 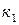=1,07, а 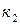=1,04. Тогда выручка увеличится и будет равна 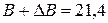, а затраты снизятся: .

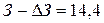Аналогично можно построить системы уравнений для поиска приростов показателе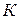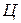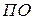й , , и 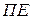. Вначале на основании рассчитанного прироста 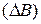и предварительно указанных выражени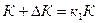й и 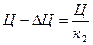составим следующую систему:

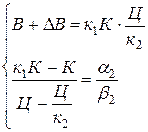
Решив данную систему, получим следующие коэффициенты:

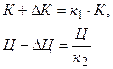
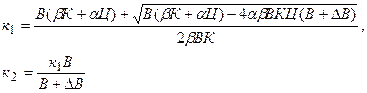
Полученные коэффициенты 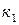и 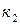позволят установить требуемые приросты для показателей К и Ц. При 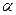=0,1, 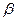=0,9 получим , .

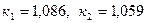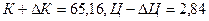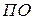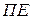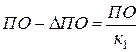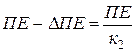Подобным же образом рассчитывается прирост для и . Записав, что и , составим следующую систему уравнений:

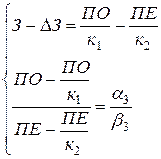
Как и ранее полученные коэффициенты используются для определения приростов 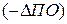и .

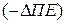Примером результатов решения задач такого рода может служить таблица, в которой указываются управляющие предписания для различных структурных подразделений.