Энтропия идеального газа

Запишем выражение первого закона термодинамики в формах (2.9) и (2.18) для идеального газа с учётом (2.35):

(2.37)

Здесь в свете обсуждённого выше учтено, что теплоёмкости идеального газа в общем случае могут зависеть от температуры.

Каждая из этих дифференциальных форм не является полным дифференциалом, однако в случае идеального газа легко проверить, что умножение их на функцию превращает их в полные дифференциалы. В самом деле, учтя уравнение состояния идеального газа , имеем

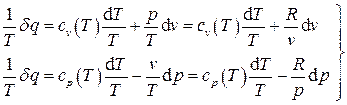. (2.38)

Вычисление перекрёстных производных этих дифференциальных форм даёт:

(2.39)

Тождественное равенство перекрёстных производных, согласно признаку (1.4), говорит о том, что дифференциал

(2.40)

является полным, а величина

(2.41)

есть некоторая новая функция состояния системы, которая по предложению немецкого учёного Р.Клаузиуса была названа энтропией. Физический смысл энтропии обсудим в главе 4. Из определения дифференциала энтропии (2.40) следует, что, по крайней мере, для идеального газа выражение для количества теплоты может быть записано в форме, аналогичной выражению для работы, т.е. как произведение некоторого потенциала (в данном случае температуры T) на изменение некоторой "координаты" (в данном случае энтропии), т.е.

, (2.42)

а количество теплоты в некотором процессе определится интегралом

. (2.43)

Использование понятия энтропии позволяет ввести в рассмотрение термодинамическую диаграмму T - s, в которой количество теплоты, согласно (2.43), определится площадью под кривой процесса, т.е. графическим изображением заданной зависимости температуры от энтропии (рис.2.3).

Следует заметить, что экспериментально замерить непосредственно энтропию невозможно, нет приборов, которыми это можно осуществить. Тем не менее энтропию можно вычислить. Например, для идеального газа из формул (2.38) интегрированием находим

. (2.44)

Здесь учтено, что энтропия принимается равной нулю при нормальных физических условиях (НФУ).

К следующему занятию курсанты должны:

ЗНАТЬ: смысл и эквивалентные формулировки первого начала термодинамики; методы вычисления теплоемкости простой термодинамической системы.

УМЕТЬ: вычислять функции состояния и теплоемкости (при постоянном давлении и при постоянном объеме) термодинамической системы.

ИМЕТЬ ПРЕДСТАВЛЕНИЕ: о принципах построения аппарата термодинамики, молекулярно-кинетическом определении идеального газа, теореме о равнораспределении энергии по степеням свободы молекулы.

 

 

Задания на самоподготовку:

· конспект лекций

· задача на применение первого начала термодинамики

 

Подпись автора

___________/ профессор каф. физики и теплообмена П.В. Скрипов

 

 

Лекция рассмотрена и одобрена на заседании кафедры

Протокол №_______ от «_____»_____________2006 г.

 

Зав. кафедрой физики и теплообмена

профессор, д.т.н. __________________ / Н.М. Барбин

«_____»______________ 2006 г.