Интеграл Бернулли в случае установившегося

Глава 5

ДИНАМИКА ИДЕАЛЬНЫХ ЖИДКИХ СРЕД

Теорема Бернулли

Жидкую среду называют идеальной, если в ней отсутствуют касательные напряжения, а действуют только нормальные напряжения. В соответствии с этим определением

После подстановки данных соотношений формула (4.28) примет вид

а поскольку

то

Скалярная величина p является давлением в точке жидкой среды. Знак минус означает, что вектор нормального напряжения направлен противоположно нормали n к площадке, проведенной через выбранную точку, т.е. . Согласно равенствам (5.1), в идеальной жидкой среде нормальное напряжение не зависит от ориентации площадки.

Модель идеальной жидкой среды не учитывает влияния внутреннего молекулярного обмена, с которым связано проявление вязкости и теплопроводности среды, но позволяет значительно упростить математическое описание движения жидкой среды и в ряде случаев находить полезные для практики решения. Поскольку уравнение неразрывности не содержит напряжений, его вид для идеальной жидкой среды не отличается от общего уравнения (4.16) неразрывности. Если к тому же идеальная жидкая среда предполагается несжимаемой, то в отсутствие источников и стоков уравнение неразрывности имеет вид уравнений (4.18) или (4.19).

Уравнения гидродинамики вследствие равенства нулю касательных напряжений упрощаются. Такие уравнения гидродинамики можно получить, принимая в уравнениях (4.31)— (4.33) , т.е. исключая члены, связанные с вязкостью среды. Уравнения движения идеальной жидкой среды, записанные в проекциях на оси декартовых координат, называют уравнениями Эйлера:

При определенных условиях систему уравнений (5.2) — (5.4) можно проинтегрировать. Полученные в результате соотношения не только раскрывают важные закономерности движения жидких сред, но часто более удобны при решении прикладных задач, чем исходные уравнения.

Принимая условия, согласно которым идеальная жидкая среда под действием потенциального поля массовых сил совершает баротропное движение, систему уравнений (5.2) — (5.4) представим в векторной форме:

Так как поле массовых сил потенциально, имеем

Баротропный характер движения среды означает, что на линии тока плотность среды является только функцией давления:

После скалярного умножения на элементарно перемещение dr вдоль линии тока уравнение (5.5) с учетом (5.6) принимает вид

При установившемся движении жидкой среды линии тока совпадают с траекториями, поэтому

и соответственно

В свою очередь,

После подстановки величин, соглано соотношениям (5.9) — (5.11), уравнение (5.8) примет вид

Чтобы исключить dp из (5.12), вводят функцию давления

в которой давление в какой-нибудь точке заторможенной жидкой среды; текущее значение давления.

С помощью (5.13) уравнение (5.12) можно записать следующим образом:

Проинтегрировав (5.14) вдоль линии тока, получим

Равенство (5.15) называется интегралом Бернулли. Постоянная в правой части (5.15), сохраняя свое значение на одной линии тока, может измениться при переходе к другой линии тока. Трехчлен (5.15) не следует считать выражением закона сохранения энергии, так как использованная при его выводе функция давления (5.13) учитывает только работу главного вектора поверхностных сил, приложенных снаружи к выделенному объему жидкой среды. Работа внутренних сил здесь не учитывается.

Если жидкая среда принята несжимаемой, то . В этом случае функцию давления (5.13) можно записать так:

С учетом (5.16) и при действии только сил тяжести (П = gz) интеграл Бернулли (5.15) принимает вид

отсюда

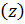Слагаемые в левой части (5.17) называют скоростным , геометрическим и пьезометрическим напором.

Равенство (5.17) выражает теорему Бернулли, которая формулируется следующим образом: при установившемся движении идеальной несжимаемой жидкости в поле сил тяжести сумма скоростного, геометрического и пьезометрического напоров сохраняет постоянное значение вдоль линии тока.

Если силы тяжести незначительны по сравнению с силами давления, то величиной z можно пренебречь и несколько упростить уравнение (5.17):

Рис. 5.1. Схема истечения несжимаемой жидкости через малое отверстие

 

Формула (5.18) указывает на важную связь между скоростью движения среды и давлением. Согласно этой формуле, при увеличении скорости среды давление понижается, а при уменьшении скорости среды давление повышается.

Теорема Бернулли позволяет не только понять и объяснить многие гидродинамические явления, ее используют также при решении различных задач. Примером служит расчет скорости истечения несжимаемой жидкости через малое отверстие в днище или стенке резервуара (рис. 5.1). Предполагая, что уровень 1 — 1 поверхности не изменяется, уравнение Бернулли (5.17) при истечении жидкости можно записать для одной из линий тока АВ в виде

Если площадь поверхности 1 — 1 значительно больше площади проходного сечения отверстия, то скорость 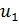будет пренебрежимо мала по сравнению с 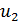. Кроме того, давление на поверхности 1 — 1 и давление в окрестности сечения 2 — 2 часто могут быть одинаковыми (например, равными атмосферному давлению). При этих условиях из приведенного уравнения следует, что

Полученное соотношение представляет собой формулу Торричелли, согласно которой скорость истечения имеет такое же значение, как скорость материальной точки, падающей с высоты H.

 

Интеграл Бернулли в случае установившегося