Изотермического и адиабатического движения совершенного газа

Газ называют совершенным, если он удовлетворяет уравнению (1.13) Клапейрона. Рассматривая движение газа, массовыми силами обычно пренебрегают, а функцию давления определяют для двух предельных случаев: изотермический процесс (температура газа постоянна); адиабатический процесс (без притока к газу теплоты извне).

При изотермическом движении газа в соответствии с уравнением (1.13) , поэтому функцию давления (5.13) можно найти следующим образом:

Уравнение Бернулли (5.15) с учетом (5.19) в отсутствие потенциала принимает вид

В случае адиабатического движения идеального газа его плотность связана с давлением соотношением

поэтому

С помощью функции (5.22) уравнение Бернулли (5.15) записывают в виде

Рис. 5.2. Схема истечения газа через малое отверстие

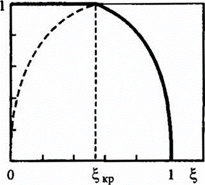
Рис. 5.3. Изменение массового расхода газа через малое отверстие в зависимости от давления после отверстия

Значения параметров и принимают постоянными для адиабатически заторможенного () идеального газа. При использовании таких постоянных величин уравнение (5.23) преобразуется в формулу Сен-Венана и Ванцеля:

Формула (5.24) позволяет выяснить различие в процессах истечения газа и несжимаемой жидкости из малого отверстия при постоянном давлении (рис. 5.2). В случае ≤ приходящийся на единицу площади массовый расход газа, согласно формулам (5.21) и (5.24), определяется в виде

где

В соответствии с формулой (5.25) при снижении давления р или повышении давления расход через отверстие увеличивается, достигая максимума при 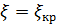(рис. 5.3). Если и , то .

В действительности участок графика, изображенного штриховой линией, не существует, так как расход при остается постоянным, равным своему максимальному значению (см. рис. 5.3). При 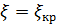скорость истечения газа достигает скорости звука. Дальнейшее уменьшение не влияет на истечение, поскольку возмущения во внешней среде не передаются по струе газа, распространяясь со скоростью звука, которая оказывается меньше скорости газа.

Таким образом, процесс истечения газа из малого отверстия отличается от процесса истечения несжимаемой жидкости. По мере приближения к единице различие в закономерностях истечения газа и несжимаемой жидкости уменьшается.

Условия возникновения сверхзвуковых течений газа можно определить, предварительно преобразовав уравнение (5.23). Выделив в уравнении соответствующую параметрам заторможенного газа величину и воспользовавшись соотношением (5.21), представим уравнение в виде

Согласно соотношению (1.27),

Поэтому при адиабатическом процессе

Формула (5.28) позволяет заменить в уравнении (5.26) величину 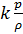квадратом скорости звука и в результате получить

Величину называют энтальпией (или теплосодержанием). Положив в (5.29) , найдем энтальпию заторможенного газа

где — скорость звука в заторможенном газе. Если скорость газа в какой-то точке достигает значения скорости звука в этом месте, энтальпия определяется через критическую скорость

Уравнение (5.29), соответственно, примет вид

Из уравнения (5.30) следует, что движение газа будет сверхзвуковым при и дозвуковым при . Данные условия обычно представляют с помощью безразмерного параметра, который называют числом Маха и обозначают Ма (или М). Число Ма равно отношению скорости и движения газа в данной точке потока к местной скорости с звука:

Согласно (5.31), поток газа будет дозвуковым при Ма < 1, звуковым при Ма = 1 и сверхзвуковым при Ма > 1. Скорость звука в воздухе вычисляют по формуле (1.29). При θ = 273 К эта скорость равна 332 м/с.