При постановке экспериментов, построении моделей часто бывает полезным предварительно установить функциональную связь между параметрами, определяющими процесс.
Если известны ФВ, характеризующие некоторый процесс, то методом сравнения размерностей можно с точностью до постоянного множителя найти уравнение, отражающее связи этих величин между собой.
Пример 1. Установить зависимость периода свободных колебаний математического маятника от его параметров.

Рис.11
Маятник характеризуется длиной  и массой груза
и массой груза  . Колебания происходят в поле сил тяжести. Его характеристика – ускорение свободного падения
. Колебания происходят в поле сил тяжести. Его характеристика – ускорение свободного падения  .Указанные величины примем в качестве основных единиц измерения. Для этого они должны обладать независимыми размерностями:
.Указанные величины примем в качестве основных единиц измерения. Для этого они должны обладать независимыми размерностями:
 ;
;
 ;
;
 .
.
Определитель, составленный из показателей степеней величин, входящих в формулы размерности:
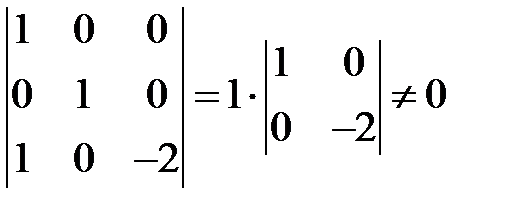 .
.
Это свидетельствует о независимости размерностей рассматриваемых физических величин.
Следовательно, период свободных колебаний маятника можно представить функцией вида:
 .
.
Величины  входят в эту функцию с показателями
входят в эту функцию с показателями  , а сама функция имеет вид степенного одночлена:
, а сама функция имеет вид степенного одночлена:
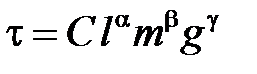 , (п.1)
, (п.1)
где  - безразмерный, неопределяемый коэффициент пропорциональности;
- безразмерный, неопределяемый коэффициент пропорциональности;
 - подлежащие определению показатели степени.
- подлежащие определению показатели степени.
Составим уравнение размерностей, выражающее равенство размерностей левой и правой частей соотношения (п.1). Так как

то можно записать:

или
 .
.
Сравнивая соответствующие показатели размерностей левой и правой частей этого равенства, получаем систему уравнений:

Отсюда:  .Подставляя найденные значения показателей в формулу (п.1), находим:
.Подставляя найденные значения показателей в формулу (п.1), находим:
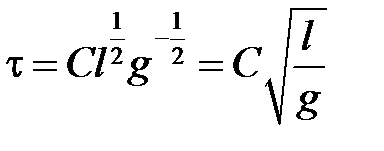 .
.
Значение коэффициента  может быть найдено из опыта (эксперимента).
может быть найдено из опыта (эксперимента).
Из решения дифференциального уравнения движения математического маятника известно, что
 .
.
В итоге получаем известную формулу для определения периода свободных колебаний маятника:
 .
.
Пример 2. Определить период свободных колебаний одномассовой системы как функцию от ее параметров: жесткости и массы.

Рис.12
Свободные колебания системы определяются следующими параметрами:  -массой,
-массой,  - жесткостью и
- жесткостью и  - перемещением массы относительно положения статического равновесия
- перемещением массы относительно положения статического равновесия  . Период свободных колебаний, в общем случае, зависит от массы
. Период свободных колебаний, в общем случае, зависит от массы  , жесткости
, жесткости  и перемещения
и перемещения  :
:
 .
.
За основные единицы примем единицы измерения величин  . Можно показать, что они обладают независимыми размерностями
. Можно показать, что они обладают независимыми размерностями
 ,
,
 ,
,
 ,
,
т.к. определитель
 .
.
Искомую функцию представим в виде степенного одночлена:
 , (п.2)
, (п.2)
где  - неопределяемый постоянный коэффициент;
- неопределяемый постоянный коэффициент;
 - показатели степени, подлежащие определению.
- показатели степени, подлежащие определению.
Левая и правая части этого равенства должны иметь одинаковую размерность. Так как  , то получаем:
, то получаем:
 .
.
Сравнивая показатели степеней при соответствующих размерностях левой и правой частей равенства, находим:

Отсюда: 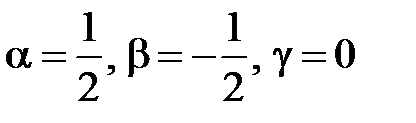 .Подставляя найденные значения показателей в (п.2), имеем:
.Подставляя найденные значения показателей в (п.2), имеем:
 .
.
Из решения уравнений движения системы известно:  .
.
Окончательно
 .
.
Пример 3. Определить период свободных колебаний поплавка в жидкости.

Рис.13
Определяющие параметры: 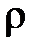 - плотность жидкости;
- плотность жидкости;  - глубина погружения поплавка;
- глубина погружения поплавка; 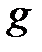 - ускорение свободного падения. Определяемый параметр:
- ускорение свободного падения. Определяемый параметр:  - период свободных колебаний.
- период свободных колебаний.
Величины  имеют независимые размерности
имеют независимые размерности
 ,
,
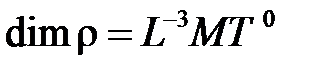 ,
,
 ,
,
т.к. определитель
 .
.
Тогда период свободных колебаний можно представить в виде степенного одночлена
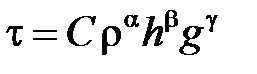 , (п.3)
, (п.3)
где  - постоянный коэффициент;
- постоянный коэффициент;
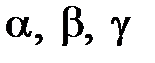 - искомые показатели степеней.
- искомые показатели степеней.
Уравнение размерностей.
Так как  , то уравнение размерностей имеет вид:
, то уравнение размерностей имеет вид:
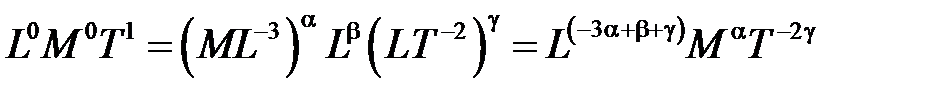 .
.
Уравнения для определения показателей степени.
Сравнивая показатели степеней при соответствующих размерностях, находим:

Отсюда 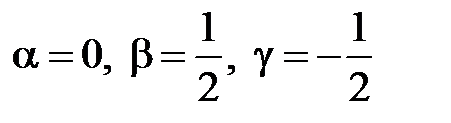 .
.
Подставим эти значения в выражение (п.3). В результате получим
 .
.
Известно, что  . Тогда
. Тогда
 .
.
Пример 4. Определить зависимость времени истечения жидкости из сосуда от его параметров (рис.14). Определяющие параметры:  - ускорение свободного падения;
- ускорение свободного падения;  - уровень жидкости в сосуде;
- уровень жидкости в сосуде;  - плотность жидкости;
- плотность жидкости;  - поперечная площадь сосуда;
- поперечная площадь сосуда; 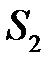 - площадь отверстия, через которое происходит истечение жидкости. Определяемый параметр:
- площадь отверстия, через которое происходит истечение жидкости. Определяемый параметр:  - время истечения жидкости из сосуда.
- время истечения жидкости из сосуда.

Рис.14
Величины  примем в качестве основных. Их размерности
примем в качестве основных. Их размерности
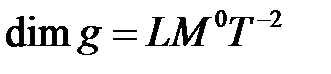 ,
,
 ,
,

являются независимым, т.к. определитель
 .
.
Будем полагать, что время истечения пропорционально  и обратно пропорционально
и обратно пропорционально  . Тогда можно принять для рассмотрения следующую функциональную зависимость:
. Тогда можно принять для рассмотрения следующую функциональную зависимость:
 . (п.4)
. (п.4)
Запишем уравнение размерностей:
Так как  то
то
 .
.
Отсюда

Решение этой системы дает: 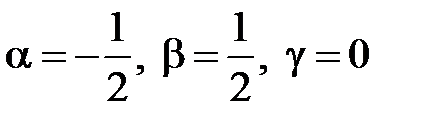 .
.
Подставляя найденные значения показателей соответствующих размерностей в выражение (п.4), находим:
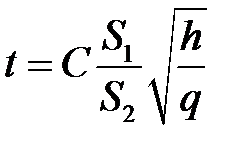 .
.
Точное решение задачи дает  . Заметим, что при отсутствии точного решения величина
. Заметим, что при отсутствии точного решения величина  может быть определена экспериментальным путем.
может быть определена экспериментальным путем.
Окончательно
 .
.
Пример 5. Установить функциональную связь силы 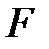 давления струи на стенку с параметрами:
давления струи на стенку с параметрами:  - площадь сечения насадка;
- площадь сечения насадка;  - скорость истечения жидкости из насадка (скорость струи).
- скорость истечения жидкости из насадка (скорость струи).

Рис.15
Определяющие параметры:  . Определяемый параметр:
. Определяемый параметр: 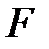 .Величины
.Величины  примем в качестве основных. Их размерности
примем в качестве основных. Их размерности
 ,
,
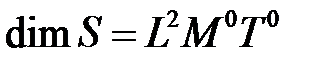 ,
,
 ,
,
являются независимыми, т.к.
 .
.
Функциональную зависимость будем искать в виде степенного одночлена
 . (п.5)
. (п.5)
Составим уравнение размерностей
Так как  , то
, то

или
 .
.
Отсюда

Тогда
 .
.
Подставляя найденные показатели в (п.5), находим:
 .
.
Известно, что  . Окончательно
. Окончательно  .
.
Пример6. Установить зависимость избыточного давления  в покоящейся жидкости в заданной точке от глубины этой точки под свободной поверхностью. Жидкость имеет плотность
в покоящейся жидкости в заданной точке от глубины этой точки под свободной поверхностью. Жидкость имеет плотность 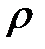 и находится в поле сил тяжести, которое характеризуется ускорением свободного падения
и находится в поле сил тяжести, которое характеризуется ускорением свободного падения  .
.

Рис.16
Избыточное давление  – определяемая величина. Величины
– определяемая величина. Величины 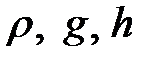 -определяющие величины, которые должны иметь независимые размерности, а их число должно быть равно числу основных единиц в системе
-определяющие величины, которые должны иметь независимые размерности, а их число должно быть равно числу основных единиц в системе  .
.
Размерность величин

являются независимыми, т.к. определитель, составленный из показателей степени,
 .
.
Связь между рассматриваемыми величинами можно представить в виде степенного одночлена
 (п.6)
(п.6)
где  - безразмерный неопределяемый коэффициент пропорциональности;
- безразмерный неопределяемый коэффициент пропорциональности;
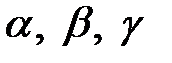 - показатели степени, подлежащие определению.
- показатели степени, подлежащие определению.
Составим уравнение размерностей

или

или
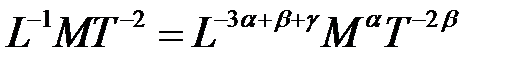 .
.
Из последнего уравнения следует система уравнений для определения показателей степени

Решая эти уравнения, находим:  .
.
Подставляя полученные значения в выражение (п.6), получаем:
 .
.
Из гидростатики известно, что  . Тогда окончательно
. Тогда окончательно
 .
.
Следует заметить, что коэффициент  может быть определен опытным путем.
может быть определен опытным путем.
Приложение 5
 2017-12-14
2017-12-14 1199
1199








