Пример 1. Течение вязкой жидкости в круглой цилиндрической трубе (рис.17).
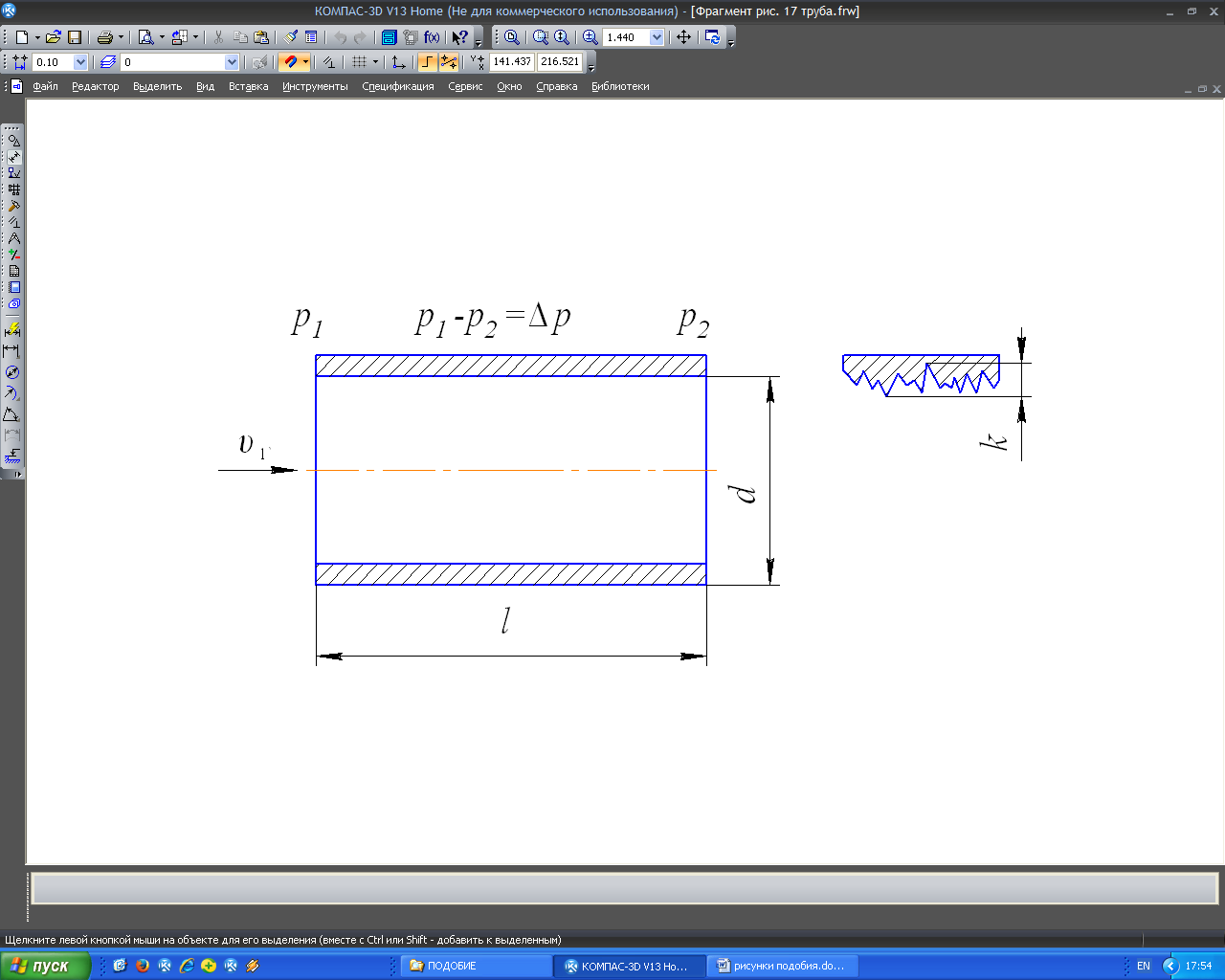
Рис.17
Искомой величиной является перепад давления на трубе 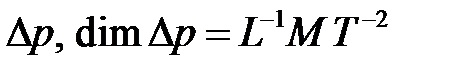 . Параметры, определяющие процесс:
. Параметры, определяющие процесс:
 - длина трубы,
- длина трубы, 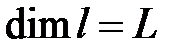 ;
;
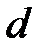 - диаметр трубы,
- диаметр трубы, 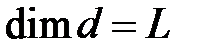 ;
;
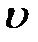 - средняя скорость движения жидкости,
- средняя скорость движения жидкости, 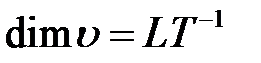 ;
;
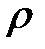 - плотность жидкости,
- плотность жидкости,  ;
;
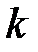 - высота выступа шероховатости,
- высота выступа шероховатости, 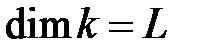 .
.
1.Список параметров рассматриваемой системы
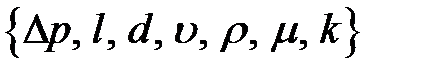 .
.
Величины 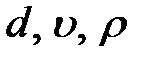 имеют независимые размерности
имеют независимые размерности
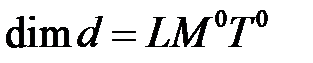 ,
,
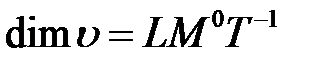 ,
,
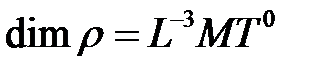 ,
,
т.к.
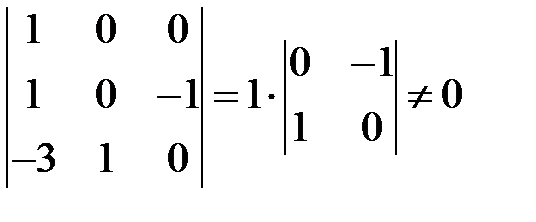 .
.
Поэтому список основных и производных величин примет вид:
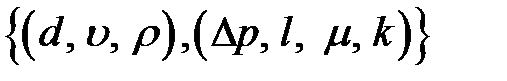 .
.
2. Количество безразмерных комплексов (критериев подобия) в соответствии с 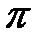 - теоремой: 7-3=4.
- теоремой: 7-3=4.
3. Определение критериев подобия
Критерий 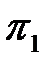 :
:
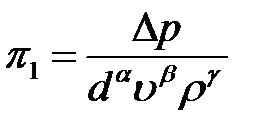 . (п.7)
. (п.7)
Составим уравнение размерностей:
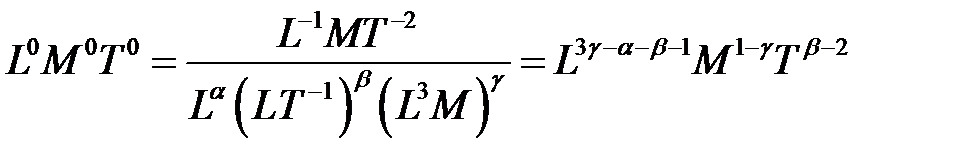 .
.
Отсюда получаем систему уравнений для определения показателей степени

Решение этих уравнений дает: 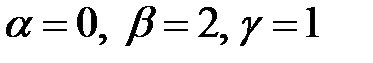 .
.
Подставляя полученные значения показателей степени в формулу (п.7), находим:
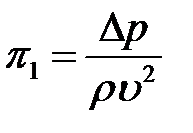 .
.
Критерий 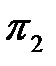 ищем в виде:
ищем в виде:
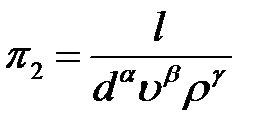 .
.
Уравнение размерностей
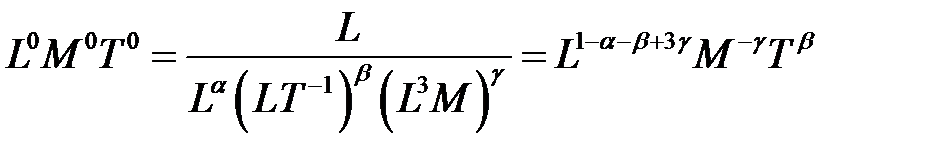 .
.
Отсюда
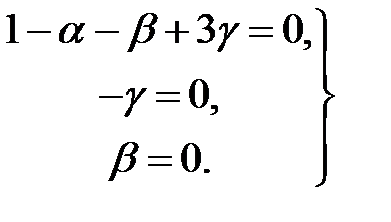
Показатели степени равны: 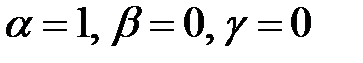 .
.
С учетом найденных значений показателей степени критерий 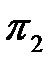 принимает вид:
принимает вид:
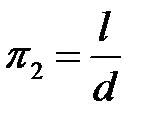 .
.
Критерий 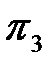
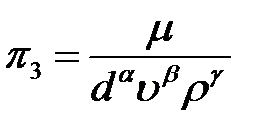 .
.
Уравнение размерностей
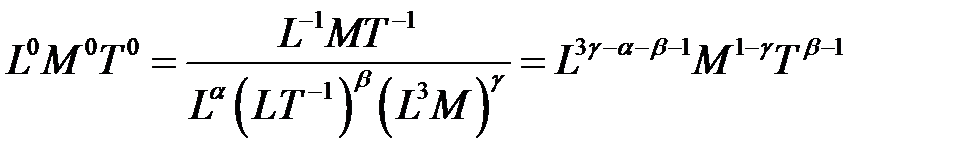 .
.
Уравнения для показателей степени
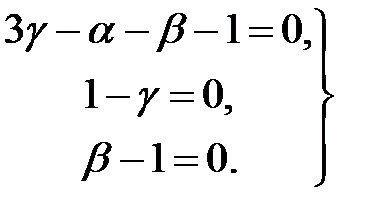
Показатели степени 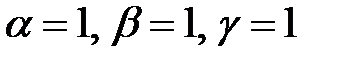 .
.
Критерий подобия
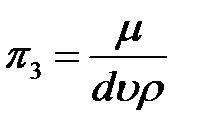 .
.
Критерий 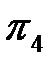 находится аналогично критерию
находится аналогично критерию 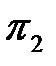 и имеет вид:
и имеет вид:
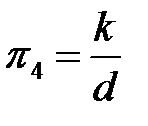 .
.
4. Критериальное уравнение запишется следующим образом:
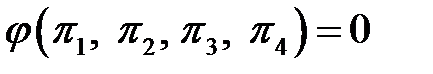
или
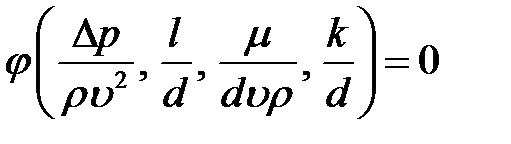 .
.
Разрешим критериальное уравнение относительно 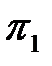 :
:
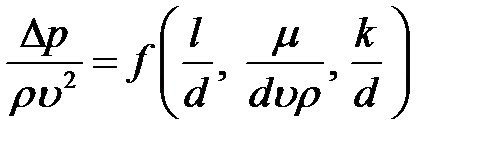 .
.
Если предположить, что течение жидкости в трубе является равномерным (характер течения и распределение скоростей не меняется вдоль трубы), то можно принять, что перепад давления будетпропорционален длине трубы. Тогда параметр 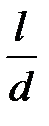 может быть вынесен за знак функции в виде множителя:
может быть вынесен за знак функции в виде множителя:
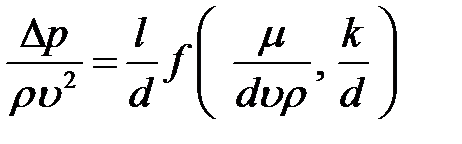 .
.
Полученная формула может быть приведена к формуле Дарси-Вейсбаха для потерь напора по длине трубы. Принимая во внимание, что 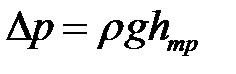 , получим:
, получим:
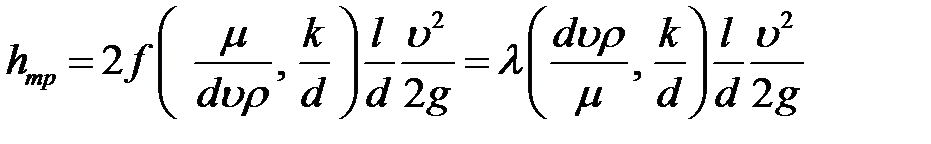 ,
,
где 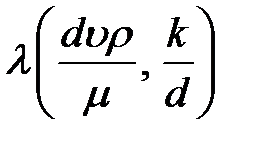 - коэффициент Дарси, зависящий от числа Рейнольдса
- коэффициент Дарси, зависящий от числа Рейнольдса 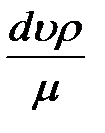 и относительной шероховатости
и относительной шероховатости 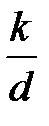 внутренней поверхности трубы.
внутренней поверхности трубы.
Пример 2. Момент трения вращающегося диска (рис. 18).
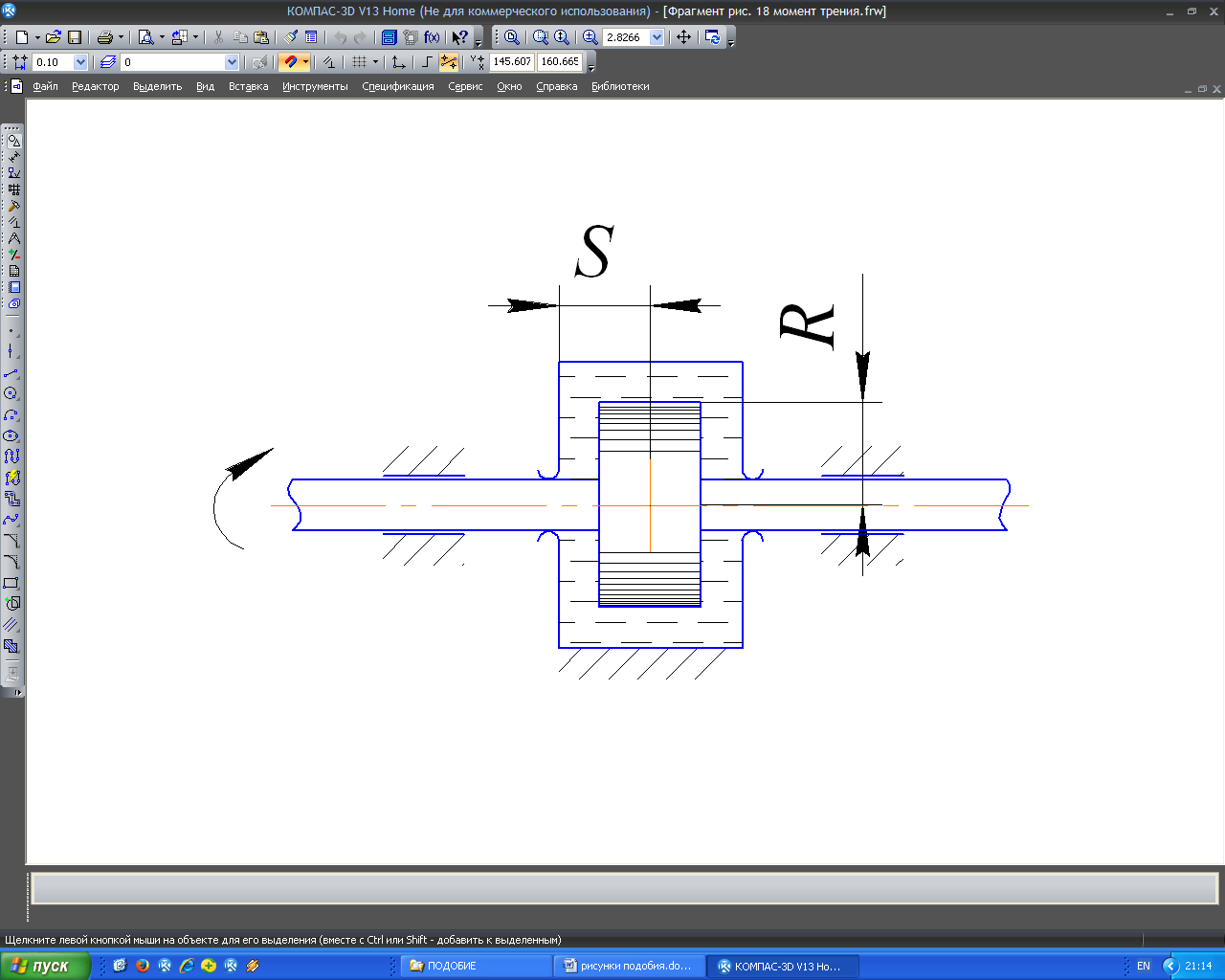
Рис. 18
Искомая величина – момент на оси  ,
, 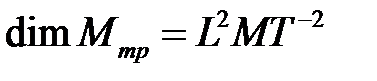 .
.
Параметры, определяющие процесс:
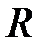 - радиус диска,
- радиус диска, 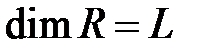 ;
;
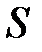 - расстояние до стенки камеры,
- расстояние до стенки камеры, 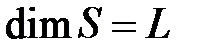 ;
;
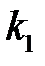 - шероховатость диска,
- шероховатость диска, 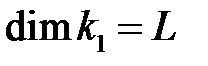 ;
;
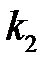 - шероховатость стенки камеры,
- шероховатость стенки камеры, 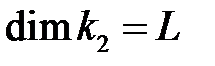 ;
;
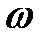 - угловая скорость,
- угловая скорость, 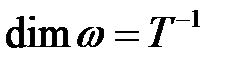 ;
;
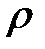 - плотность жидкости,
- плотность жидкости, 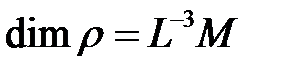 ;
;
1. Список параметров системы
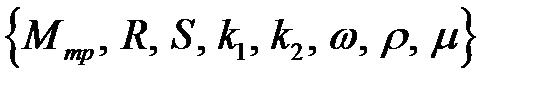 .
.
Список основных и производных величин
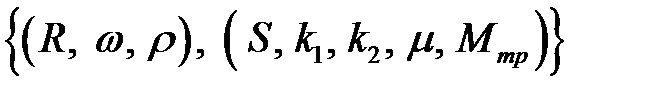 .
.
2. Количество критериев подобия: 8-3=5.
3. Определение критериев подобия.
Критерий 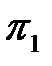 :
:
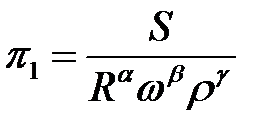 ;
;
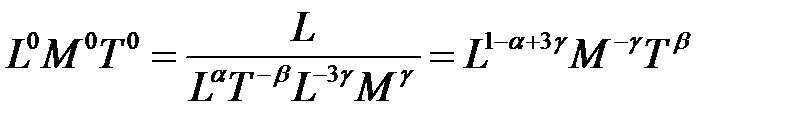 ;
;
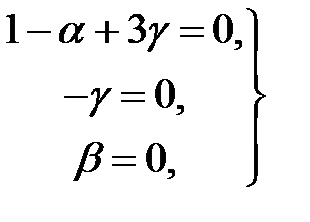 ;
;
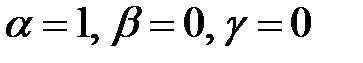 ;
;
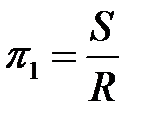 .
.
Критерии 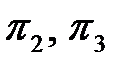 . Находятся аналогично критерию
. Находятся аналогично критерию 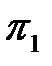 и имеют вид:
и имеют вид:
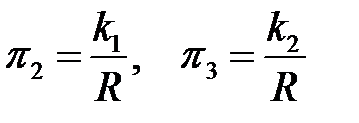 .
.
Критерий 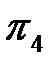 .
.
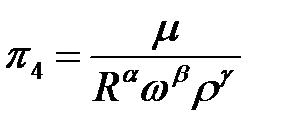 ;
;
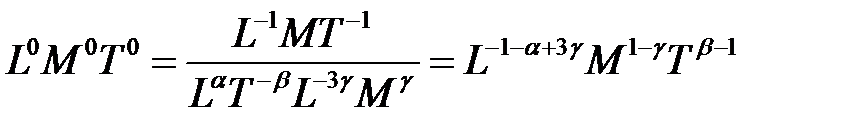 ;
;
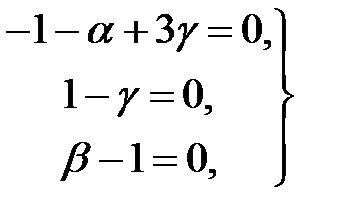 ;
;
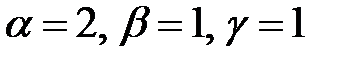 ;
;
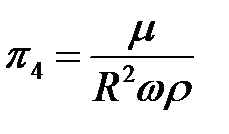 .
.
Критерий 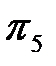 .
.
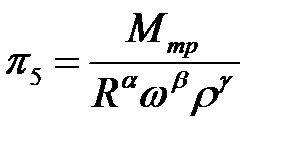 ;
;
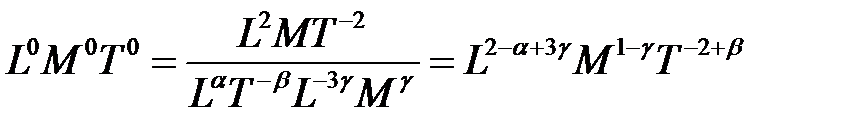 ;
;
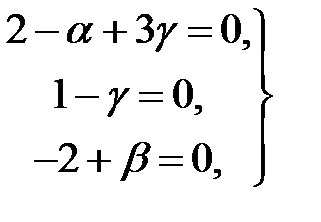 ;
;
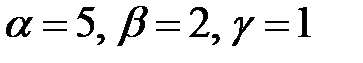 ;
;
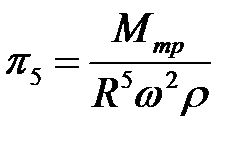 .
.
4. Критериальное уравнение
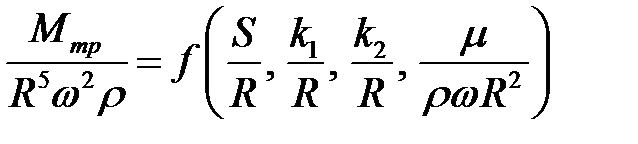 .
.
Отсюда
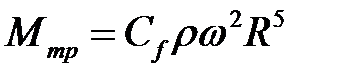 ,
,
где 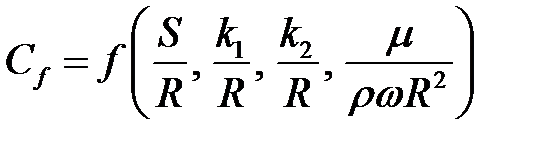 .
.
Рассмотрим величину 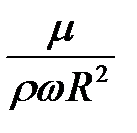 . Этот критерий можно заменить критерием Рейнольдса
. Этот критерий можно заменить критерием Рейнольдса 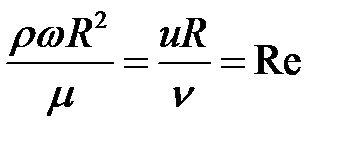 , где
, где 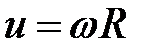 - окружная скорость диска. Тогда
- окружная скорость диска. Тогда
 .
.
Величина 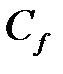 может быть определена экспериментальным путем.
может быть определена экспериментальным путем.
Пример 3. Вихревое обтекание тела (рис.19).
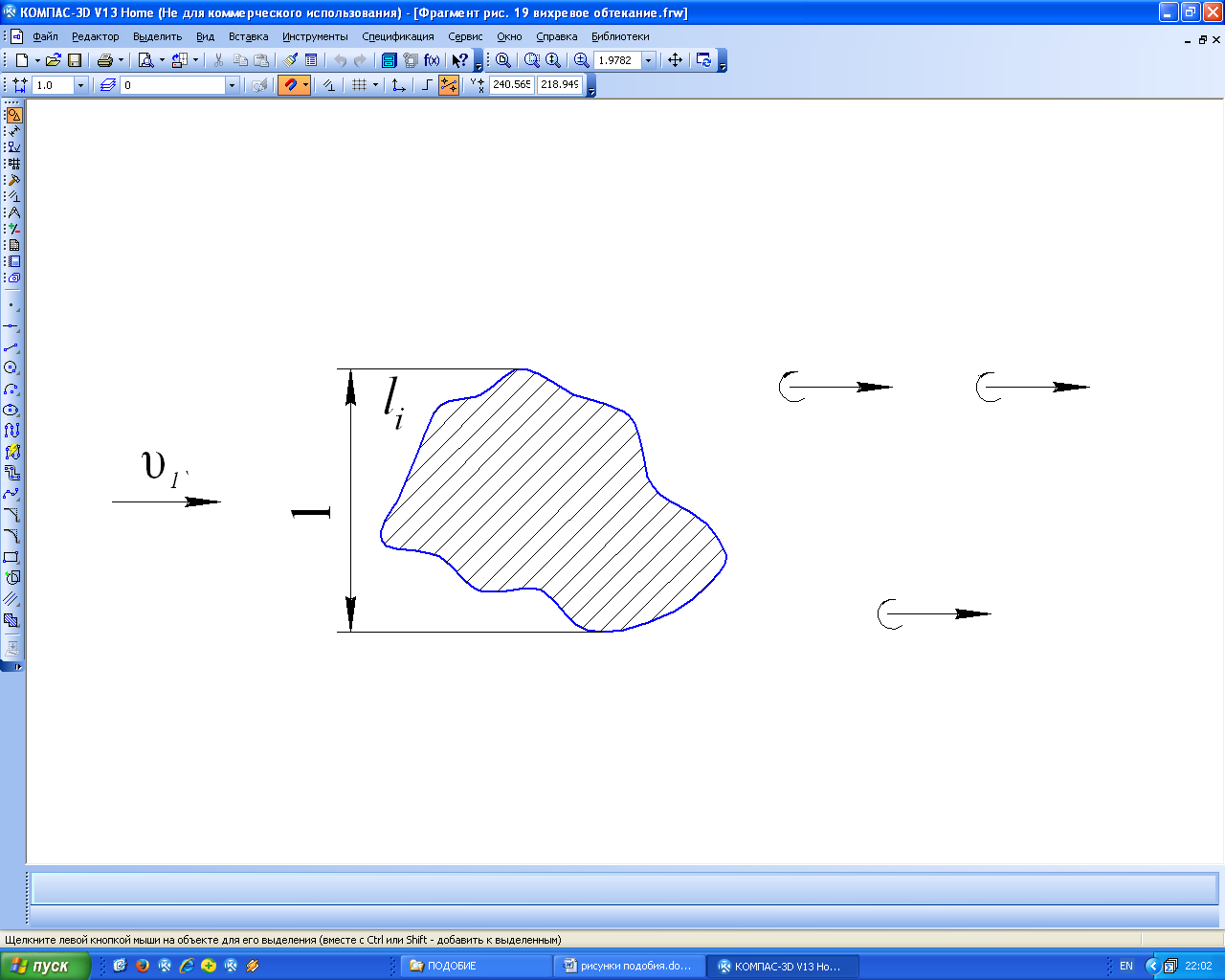
Рис.19
Необходимо определить период срыва вихрей 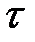 ,
, 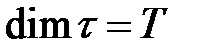 .
.
1. Процесс характеризуется следующими параметрами
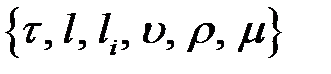 .
.
Здесь:  - характерный размер,
- характерный размер, 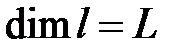 ;
; 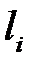 - размер, определяющий форму тела,
- размер, определяющий форму тела, 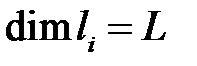 ;
; 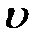 - скорость обтекающего потока,
- скорость обтекающего потока, 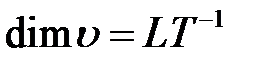 ;
; 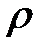 - плотность жидкости,
- плотность жидкости, 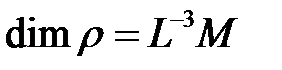 ;
; 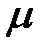 - динамическая вязкость,
- динамическая вязкость, 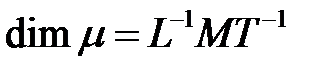 .
.
Список основных и производных величин
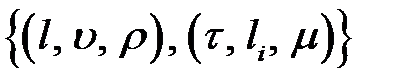 .
.
2. Количество критериев: 6-3=3.
3. Определение критериев подобия.
Критерий 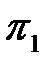
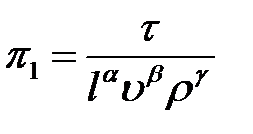 ;
;
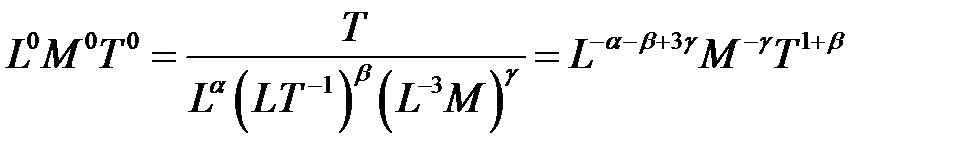 ;
;
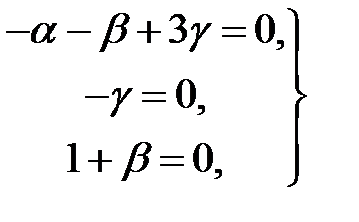 ;
;
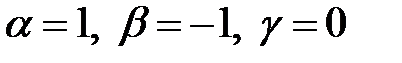 ;
;
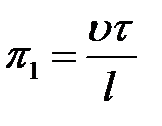 .
.
Критерий 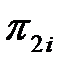
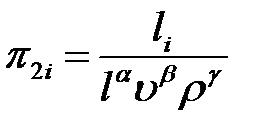 ;
;
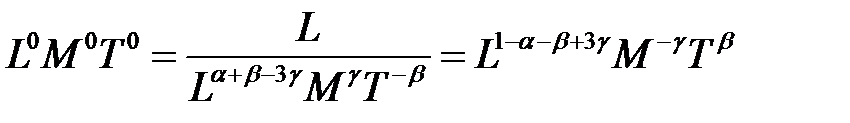 ;
;
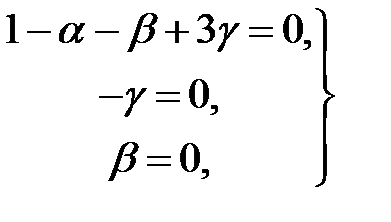 ;
;
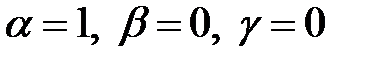 ;
;
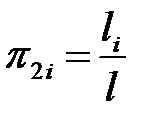 .
.
Критерий 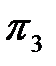
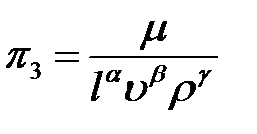 ;
;
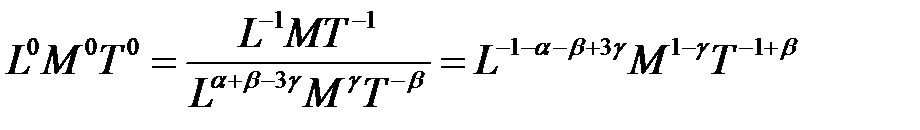 ;
;
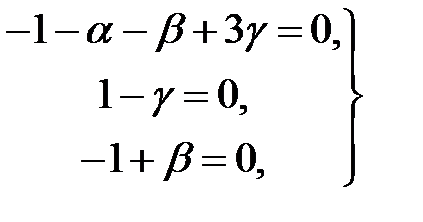 ;
;
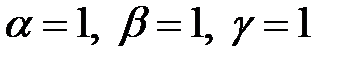 ;
;
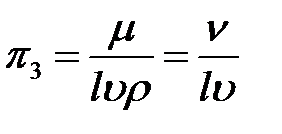 .
.
4. Критериальное уравнение
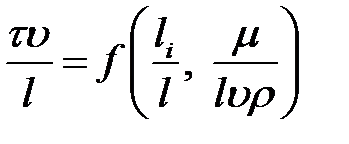 .
.
Отсюда
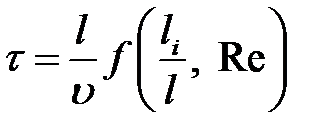 ,
,
где 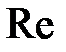 – число Рейнольдса.
– число Рейнольдса.
Величина 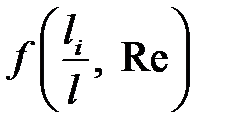 может быть определена экспериментальным путем.
может быть определена экспериментальным путем.
Пример 4. Сопротивление сферы при обтекании потоком вязкой жидкости. Искомая величина – сила сопротивления 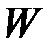 ,
, 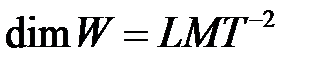 . Параметры, определяющие процесс:
. Параметры, определяющие процесс: 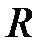 - радиус сферы,
- радиус сферы, 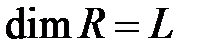 ;
; 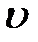 - скорость обтекания,
- скорость обтекания, 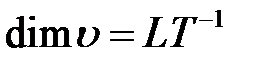 ;
; 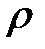 - плотность жидкости,
- плотность жидкости, 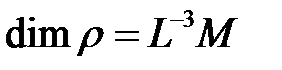 ;
; 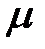 - динамическая вязкость,
- динамическая вязкость, 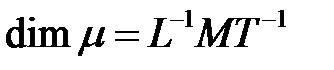 .
.
1. Список параметров, характеризующих процесс:
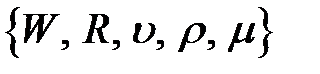 .
.
Основные и производные величины
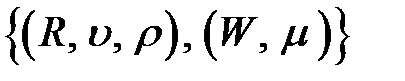 .
.
2. Количество критериев: 5-3=2.
3. Определение критериев.
Критерий 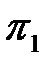
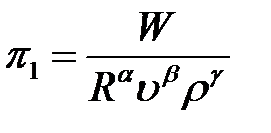 ;
;
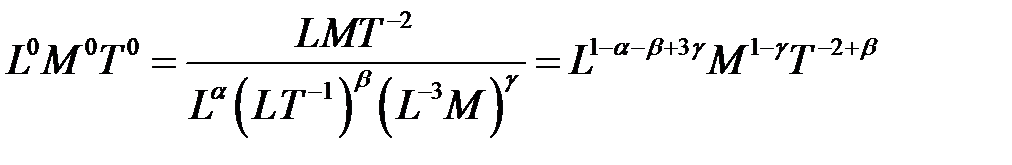 ;
;
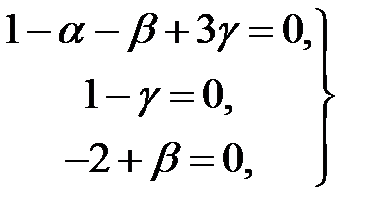 ;
;
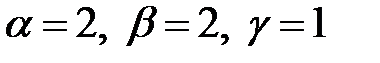 ;
;
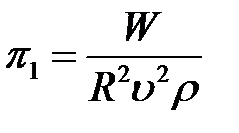 .
.
Критерий 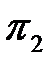
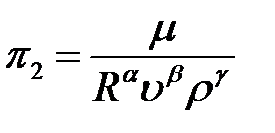 ;
;
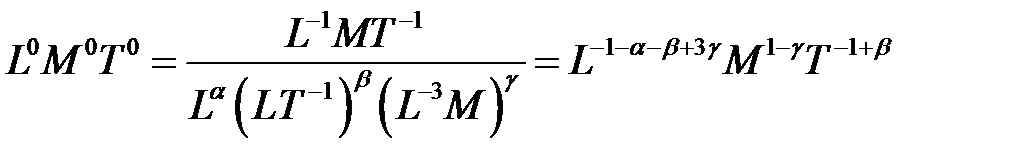 ;
;
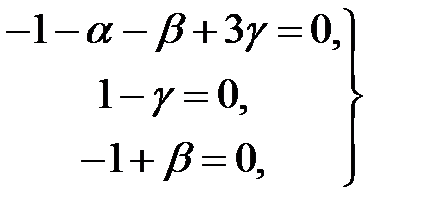 ;
;
 ;
;
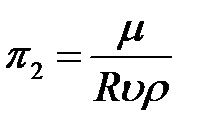 .
.
4. Критериальное уравнение
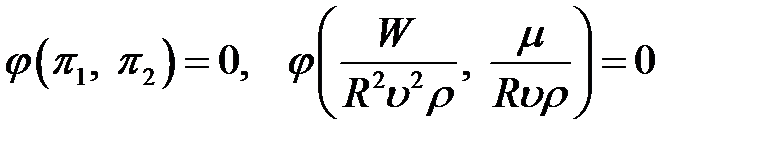
или
 ,
,
где 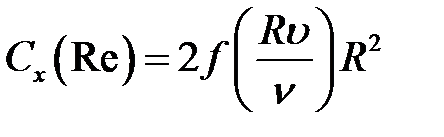 - коэффициент сопротивления, определяемый экспериментально.
- коэффициент сопротивления, определяемый экспериментально.
Пример 5. Задача Стокса о падении шара малых размеров в вязкой среде под действием силы тяжести. Предполагается, что падение шара не вызывает турбулентности. Список параметров, характеризующих процесс:
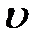 - скорость шара,
- скорость шара, 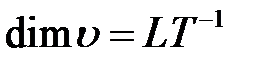 ;
;
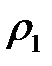 - плотность шара,
- плотность шара, 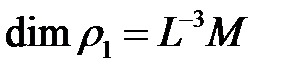 ;
;
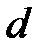 - диаметр шара,
- диаметр шара, 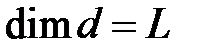 ;
;
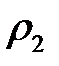 - плотность среды,
- плотность среды, 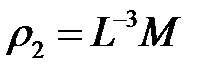 ;
;
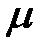 - динамическая вязкость среды,
- динамическая вязкость среды, 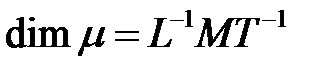 ;
;
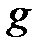 - ускорение свободного падения,
- ускорение свободного падения, 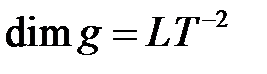 .
.
1. Список основных и производных величин
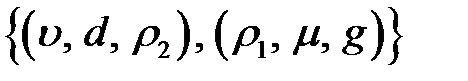 .
.
2. Число критериев: 6-3=3.
3. Определение критериев.
Критерий 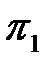
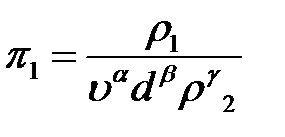 ;
;
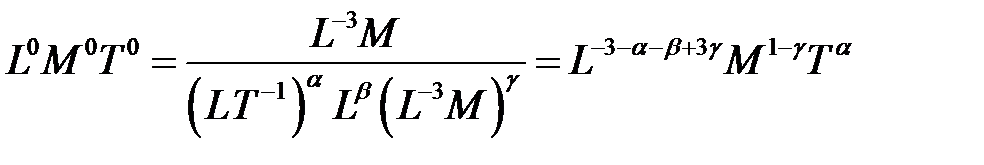 ;
;
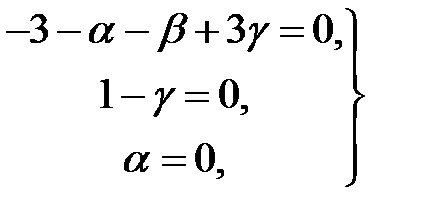 ;
;
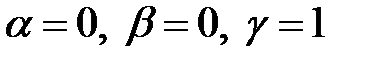 ;
;
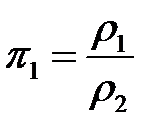 .
.
Критерий 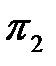
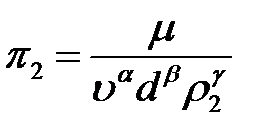 ;
;
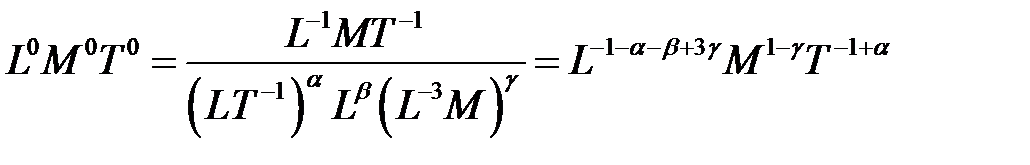 ;
;
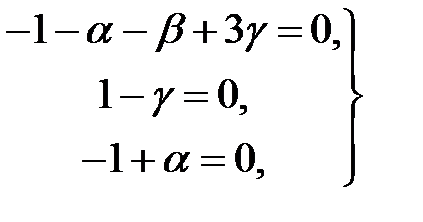 ;
;
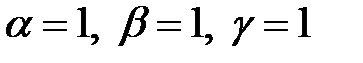 ;
;
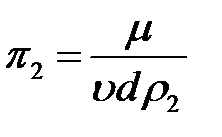 .
.
Критерий 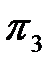
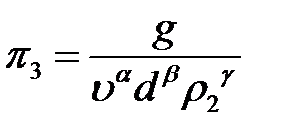 ;
;
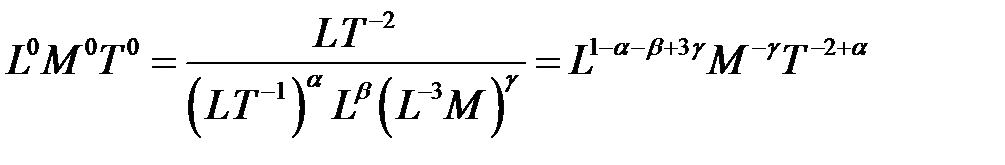 ;
;
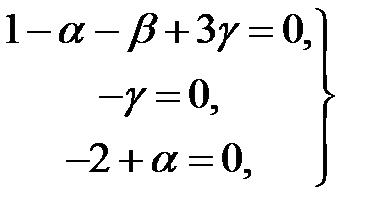 ;
;
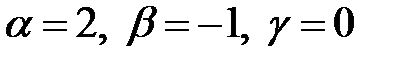 ;
;
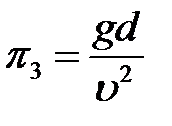 .
.
4. Критериальное уравнение
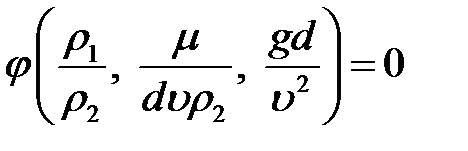
или
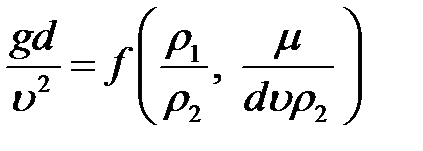 .
.
Отсюда
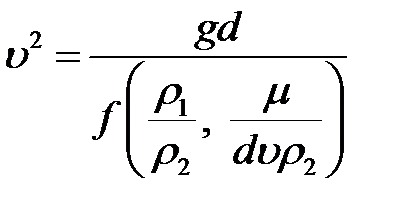
или
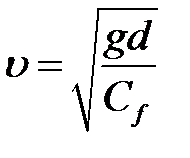 ,
,
где 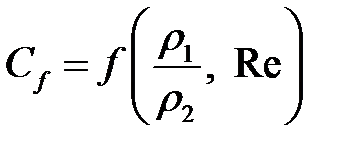 - коэффициент, определяемый экспериментально;
- коэффициент, определяемый экспериментально;
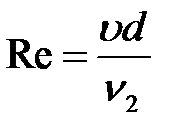 - число Рейнольдса.
- число Рейнольдса.
Приложение 6
 2017-12-14
2017-12-14 1105
1105

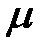 -
- 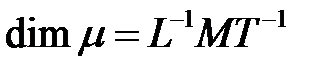 ;
;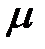 -
- 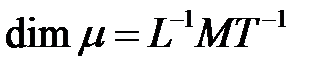 .
.






