2017-10-25
1617
На рис. 4.2 представлена цилиндрическая стенка (труба) длиной l с коэффициентом теплопроводности 
. Известны её внутренний d 1и наружный d 2 диаметры. Заданы значения средней температуры текущего внутри трубы горячего теплоносителя Т т1 (штриховая линия на рис. 4.2) и температуры холодного теплоносителя Т т2, а также коэффициентов теплоотдачи от горячего теплоносителя в стенку 
и от стенки - в холодный теплоноситель 
.
Будем считать, что распространение теплоты происходит только в радиальном направлении, т.е. распространением теплоты вдоль оси трубы будем пренебрегать. Характер изменения температуры теплоносителей и стенки по направлению её радиуса показан для этого случая на рис. 4.2, где T 
и T 
— температуры стенки соответственно на внутренней и наружной её поверхностях.
На стационарном режиме тепловой поток Q 
от горячего теплоносителя в стенку равен тепловым потокам в стенке Q 
и от стенки в холодный теплоноситель Q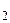 
. Следует отметить, что соответствующие плотности тепловых потоков (q , q и q 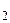) в данном случае не равны между собой, так как площадь поверхности, через которую проходит один и тот же тепловой поток Q, с увеличением радиуса возрастает.
Для участка трубы длиной l имеем:
Q 
;
Q 
;
Q 
.
Отсюда при Q 
получим
;
;
.
Просуммировав эти соотношения, получим
,
Откуда Q = 
(
) = 
,
где: k 
- линейный коэффициент теплопередачи;
R 
- общее линейное тепловое сопротивление.
В расчётах используется также линейная плотность теплового потока
q 
= 
.
Определив значение q 
, можно так же, как для плоской стенки, найти значения температур на поверхностях цилиндрической стенки
Т 
, Т 
.
Для многослойной цилиндрической стенки, состоящей из n слоев, значения Q и q определяются также, но общее линейное тепловое сопротивление в этом случае определяется с учётом тепловых сопротивлений всех слоёв и контактных тепловых сопротивлений между ними
R 
+ 
Здесь 
/ d 
― линейное контактное тепловое сопротивление между слоями i и j = i +1 многослойной цилиндрической стенки.
Тепловая изоляция
При создании и эксплуатации летательных аппаратов возникает необходимость уменьшить тепловые потоки от некоторых их элементов во внешнюю среду или, наоборот, из внешней среды к ним. Для этого на стенки, окружающие эти элементы конструкции, наносится снаружи (иногда изнутри) слой материала с низким коэффициентом теплопроводности (теплоизолятор).
Для теплоизоляции ёмкостей, предназначенных для хранения жидкого водорода, кислорода и других криогенных веществ, применяются вакуумно-порошковые прослойки, у которых коэффициент теплопроводности достигает значений 0,001…0,0003 Вт/(м×К).
Определим толщину теплоизоляционного покрытия, необходимого для уменьшения тепловых потерь q 
до заданного (допустимого) значения.
 |
| Рис. 4.3. Тепловая изоляция плоской и цилиндрической стенки |
Рассмотрим плоскую стенку толщиной 
, покрытую тепловой изоляцией (рис. 4.3 а). Температуры изолируемой и внешней среды соответственно равны 
и 
, а коэффициенты теплоотдачи - и . Известны коэффициенты теплопроводности стенки и изоляции 
. Тепловое сопротивление контакта будем считать отсутствующим (R 
.
По заданному значению 
может быть определено потребное (допустимое) значение коэффициента теплопередачи для стенки с тепловой изоляцией k 
.
Так как рассматривается двухслойная стенка, то
k 
Отсюда находится необходимая толщина теплоизоляционного покрытия для плоской стенки 
.
Видно, что для плоской стенки, чем толще слой изоляции и чем меньше коэффициент теплопроводности изолирующего материала, тем меньше коэффициент теплопередачи через стенку.
