2017-12-14
888
Если уравнение имеет вид
то замена 
приводит его к квадратному, поскольку 
() и.
Если вместо слагаемого 
будет 
, то нужная замена будет 
.
Уравнение
сводится к квадратному уравнению
представлением 
как 
. Легко проверить, что 
при которых 
, не являются корнями уравнения, и, сделав замену 
, уравнение сводится к квадратному.
Пример Решить уравнение 
.
Решение. Перенесем 
в левую часть, заменим ее на 
, 
и 
выразим через 
и 
.
После упрощений получим: 
. Разделим почленно на 
, сделаем замену :
Возвращаясь к , найдем 
.
Уравнения, однородные относительно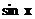 
, 
Рассмотрим уравнение вида
где 
, 
, 
,..., 
, 
--- действительные числа. В каждом слагаемом левой части уравнения степени одночленов равны 
, т. е. сумма степеней синуса и косинуса одна и та же и равна . Такое уравнение называется однородным относительно и , а число называется показателем однородности.
Ясно, что если 
, то уравнение примет вид:
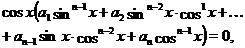
решениями которого являются значения , при которых , т. е. числа 
, 
. Второе уравнение, записанное в скобках также является однородным, но степени на 1 ниже.
Если же 
, то эти числа не являются корнями уравнения.
При получим: , 
и левая часть уравнения (1) принимает значение 
.
Итак, при , 
и 
, поэтому можно разделить обе части уравнения на 
. В результате получаем уравнение:
которое, подстановкой 
легко сводится к алгебраическому:
Однородные уравнения с показателем однородности 1. При 
имеем уравнение 
.
Если 
, то это уравнение равносильно уравнению 
, 
, откуда 
, .
Пример Решите уравнение 
.
Решение. Это уравнение однородное первой степени . Разделим обе его части на получим: 
, 
, 
, .
Ответ. 
.
Пример При 
получим однородное уравнение вида
Решение.
Если , тогда разделим обе части уравнения на , получим уравнение 
, которое подстановкой легко приводится к квадратному: 
. Если 
, то уравнение имеет действительные корни 
, 
. Исходное уравнение будет иметь две группы решений: 
, 
, 
.
Если 
, то уравнение не имеет решений.
Пример Решите уравнение 
.
Решение. Это уравнение однородное второй степени. Разделим обе чести уравнения на , получим: 
. Пусть , тогда 
, 
, 
. 
, 
, ; 
, 
, .
Ответ. 
.
К уравнению вида сводится уравнение
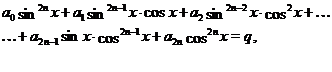
Для этого достаточно воспользоваться тождеством 
В частности, уравнение 
сводится к однородному, если заменить на 
, тогда получим равносильное уравнение: 
Пример Решите уравнение 
.
Решение. Преобразуем уравнение к однородному:
Разделим обе части уравнения на 
, получим уравнение:
Пусть , тогда приходим к квадратному уравнению: 
, 
, 
, 
, 
.
Ответ. 
.
Пример Решите уравнение 
.
Решение. Возведем обе части уравнения в квадрат, учитывая, что они имеют положительные значения: 
, 
,
Пусть , тогда получим 
, 
, 
.
Ответ. 
.
Уравнения, решаемые с помощью тождеств 
Полезно знать следующие формулы:
Пример Решить уравнение 
.
Решение. Используя, получаем
Ответ. 
Предлагаем не сами формулы, а способ их вывода:
следовательно,
.
Аналогично, 
.
Пример Решить уравнение 
.
Решение. Преобразуем выражение 
:
.
Уравнение запишется в виде:
Принимая 
, получаем 
. 
, 
. Следовательно
Ответ. 
.
ЗАКЛЮЧЕНИЕ
В данном реферате были рассмотрены методы решения тригонометрических уравнений и неравенств, как простейших, так и олимпиадного уровня. Были рассмотрены основные методы решения тригонометрических уравнений и неравенств, причем, как специфические --характерные только для тригонометрических уравнений и неравенств,- так и общие функциональные методы решения уравнений и неравенств, применительно к тригонометрическим уравнениям.
В работе приведены основные теоретические сведения: определение и свойства тригонометрических и обратных тригонометрических функций; выражение тригонометрических функций через другие тригонометрических функции, что очень важно для преобразования тригонометрических выражений, в особенности содержащих обратные тригонометрические функции; кроме основных тригонометрических формул, хорошо известных из школьного курса, приведены формулы упрощающие выражения, содержащие обратные тригонометрические функции. Рассмотрены решение элементарных тригонометрических уравнений, метод разложения на множители, методы сведения тригонометрических уравнений к алгебраическим. Ввиду того, что решения тригонометрических уравнений можно записать несколькими способами, и вид этих решений не позволяет сразу установить, являются ли эти решения одинаковыми или различными, рассмотрена общая схема решения тригонометрических уравнений и подробно рассмотрено преобразование групп общих решений тригонометрических уравнений.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Выгодский Я.Я., Справочник по элементарной математике. /Выгодский Я.Я. --- М.: Наука, 1970.
Игудисман О., Математика на устном экзамене/ Игудисман О. --- М.: Айрис пресс, Рольф, 2001.
Азаров А.И., уравнения/Азаров А.И., Гладун О.М., Федосенко В.С. --- Мн.: Тривиум, 1994.
Литвиненко В.Н., Практикум по элементарной математике / Литвиненко В.Н.--- М.: Просвещение, 1991.
Шарыгин И.Ф., Факультативный курс по математике: решение задач/ Шарыгин И.Ф., Голубев В.И. --- М.: Просвещение, 1991.
Бардушкин В., Тригонометрические уравнения. Отбор корней/В. Бардушкин, А. Прокофьев.// Математика, №12, 2005 с. 23--27.
Василевский А.Б., Задания для внеклассной работы по математике/Василевский А.Б. --- Мн.: Народная асвета. 1988. --- 176с.
Сапунов П. И., Преобразование и объединение групп общих решений тригонометрических уравнений/Сапунов П. И. // Математическое просвещение, выпуск №3, 1935.
Бородин П., Тригонометрия. Материалы вступительных экзаменов в МГУ[текст]/П.Бородин, В.Галкин, В.Панфёров, И.Сергеев, В.Тарасов // Математика №1, 2005 с. 36--48.
Самусенко А.В., Математика: Типичные ошибки абитуриентов: Справочное пособие/Самусенко А.В., Казаченок В.В.--- Мн.: Вышейшая школа, 1991.
Азаров А.И., Функциональный и графический методы решения экзаменационных задач/Азаров А.И., Барвенов С.А.,--- Мн.: Аверсэв, 2004.
